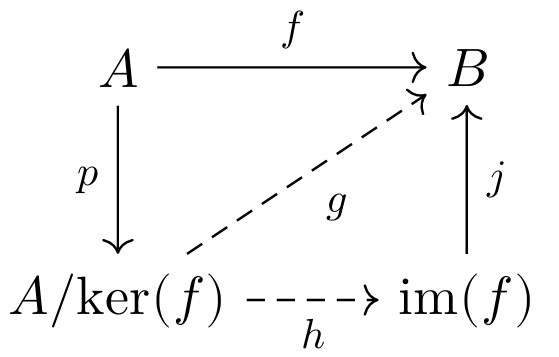Chapter 1
Existence of the Equivalence Closure
Proposition 1.85: Existence of the Equivalence Closure
Every relation
has an equivalence closure .
Proof
Consider the property
of being an equivalence relation. Every relation on is contained in the total relation of , which is an equivalence relation. Next, we prove that the intersection of any set of equivalence relations on is an equivalence relation on . Let
. We need to show that is reflexive, symmetric, and transitive.
Reflexivity: Since every equivalence relation is reflexive, we have
for every index . Therefore, , and is reflexive. Symmetry: This can be proved by observing that
where:
- The first equality follows from the definition of
. - The second equality follows from compatibility of opposites with intersections.
- The third equality follows from the fact that every
is symmetric, hence . - The last equality follows from the definition of
. Transitivity: This can be proved by observing that
where:
The first equality follows from the definition of
. The second equality follows from the fact that
(formula 1.108). The third equality follows from the fact that the intersection on the right is taken on a subset of the set of indices of the intersection on the left,
, and thus contains the intersection on the left. The fourth equality follows from the fact that
because every is an equivalence relation. The last equality follows from the definition of
. By applying proposition 1.84 to the property of being an equivalence relation, we obtain that every relation on
has an equivalence closure.
Stability of Equivalences
Proposition 1.100: Stability of Equivalences
Equivalence relations are stable under inverse images. More precisely, if
is any function, the inverse image along of every equivalence relation on is an equivalence relation on
Proof
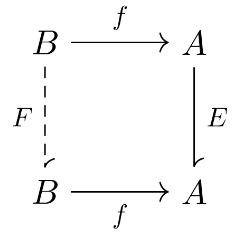
Assume, in the diagram below, that
is an equivalence relation on and that is its inverse image along .
We prove that
is an equivalence relation on .
is reflexive because where:
- the first inclusion follows from the fact
is a function; - the second equality from the fact that
is neutral for the product; - the last inclusion from the fact that
because is reflexive and from compatibility of the product with inclusion. Since
is reflexive.
is symmetric because where:
the first equality follows from the definition of
; the second from the compatibility of the opposite with products;
the third from the fact that the opposite is involutory and
is symmetric; the last from the definition of
.
is transitive, because where:
- the first equality follows from the definition of
; - the second inclusion from the fact that
because is a function and from compatibility of the product with inclusion; - the third equality from the fact that
is neutral for the product; - the fourth from the fact that
is an equivalence relation; - the last from the definition of
.
First Isomorphism Theorem
Theorem 1.151: First Isomorphism Theorem
If
is a function, then induces an isomorphism defined by the formula
.
Proof
Consider the diagram below, in which
is the projection on the quotient set, defined by the formula , and is the inclusion of the image of in defined by the formula .
Observe that
is surjective and ; by the epi factorization lemma, there exists a unique function such that . Moreover,
, so that is a monomorphism and . Since is injective and , the mono factorization lemma yields a unique function such that . By the lemma, so that is a monomorphism and , so that is an epimorphism. Thus, is an isomorphism. Since
, we have .
Chapter 2
Hintikka’s lemma
Lemma 2.109: Hintikka
Every Hintikka set
is satisfiable.
Proof
Define a valuation
setting, for every variable and let
We prove that
by structural induction for uniform notation. Observe that all formulas belong to by definition of ; thus, we only need to use structural induction on formulas .
Atomic formulas and their negations.
- If
is a variable, then by definition of , hence . - If
is the negation of a variable, then by the first property in the definition of Hintikka set, hence by definition of , hence by the semantics of negation, hence . - If
is a constant, it must be by the second condition in the definition of Hintikka set; therefore by the semantics of truth and . - If
is the negation of a constant, it must be by the second condition in the definition of Hintikka set; but then by the semantics of falsehood and negation and therefore . Double negation. Suppose
and . Then (condition 3 of definition 2.108) and since we must have . But then and .
-formulas. Suppose is an -formula with . Then (definition 2.108, condition 4) and since both are in we must have . But then and .
-formulas. Suppose is a -formula with . Then for at least one index (definition 2.108, condition 5) and since we must have for this index . But then and . Thus
(theorem 2.76); therefore if then , so that and is satisfiable.
Maximal elements are Hintikka
Proposition 2.110
If
is a consistency poset, every maximal element is a Hintikka set.
Proof
This is a straightforward application of the definition of consistency poset and of maximal element.
- If
then because is a consistency poset. because is a consistency poset. - Suppose
. The because is a consistency poset. However, and is maximal in , hence and . - Suppose
. Since is a consistency poset, . But and is maximal, hence and . - If
, the for at least one index because is a consistency poset. Since and is maximal, and therefore .
Resolution is Sound
Theorem 2.178
The resolution calculus is sound:
Proof
We first prove that the inference rules of the calculus (definition 2.172) are sound, in the sense that if a valuation
satisfies the premises of a rule in the formulas
Name Rule Hypotheses False Double negation -expansion -expansion Resolution Cut then it also satisfies the conclusion.
Falsehood. If
, then where is a generalized clause not containing . By the substitution lemma, and therefore if
, then . The case for is identical, because . Double negation. If
then where is a generalized clause not containing . By the substitution lemma, and therefore if
, then .
-expansion. If then where is a generalized clause not containing , and therefore if
, then for .
-expansion. If then where is a generalized clause not containing . Therefore, and if
, then . Resolution. Assume
and . Then and where and are generalized clauses with and , so that . There are two possibilities:
- if
then and since , we must have and therefore ; - if
then, since , we must have and therefore . As a consequence, if
is a set of formulas and then also satisfies every expansion of . Thus, if has a closed expansion then it is unsatisfiable, because no valuation satisfies the empty clause. Thus, if then has a closed expansion and is therefore unsatisfiable; therefore, .
Resolutions Defines a Finitary Inference Relation
Proposition 2.183
The resolution inference is a finitary inference relation.
Proof
- Finiteness. This amounts to prove that
has a closed expansion if and only if it has a finite subset which has a closed expansion. However, every expansion of is also an expansion of . And conversely, every expansion of has finite length, hence uses the assumption rule only finitely many times, hence is an expansion of a finite subset . - Identity. If
, then has a closed expansion as shown in the table below, hence .
STEP CLAUSE RULE 1 assumption 2 assumption 3 1,2, resolution
- Consistency. It suffices to observe that
where the first equivalence follows from the definition of and the second from lemma 2.182 . - Composition. We use proposition 2.136 and prove that if
and , then .
STEP ASSERTION REASON 1. hypothesis 2. hypothesis 3. 2, lemma 2.182 4. 3, lemma 2.181 5. 4, cut inference rule 6. 1, lemma 2.182 7. 5, 6 8. 7, lemma 2.182 To clarify step 7 in composition, observe that if in 5 we have
then we are done; otherwise and splicing such an expansion with one for we obtain a closed expansion for .