Chapter 1
Analytic Construction of the Equivalence Closure
Proposition 1.86: Analytic Construction of the Equivalence Closure
Let
be a relation on .
admits a reflexive closure . admits a symmetric closure . admits a transitive closure . Moreover,
is compatible with symmetry and transitivity, in the sense that if is symmetric or transitive, so is . Likewise, is compatible with reflexivity and is compatible with reflexivity and symmetry.
Proof
- Since
is reflexive and clearly contains . If now is reflexive and contains , we have both and , so that . This proves that is the reflexive closure of . Suppose
is symmetric. We have where:
- the first equality follows from the definition of
; - the second from compatibility of the opposite with union (proposition 1.50);
- the third from the assumption that
is symmetric and the fact that the identity relation is symmetric; - the last by the definition of
. Assume
is transitive. Then where:
- the first equality follows from the definition of
; - the second from compatibility of the product with union (proposition 1.39);
- the third inclusion from the assumption that
is transitive, i.e. and the fact that the identity is neutral for the product; - the fourth from idempotency of union;
- the last form the definition of
. This proves that
is transitive.
- By definition
; moreover, is symmetric, because where
- the first equality follows from the definition of
; - the second from compatibility of the opposite with unions (proposition 1.50);
- the third from the involutory property of the opposite (proposition 1.48);
- the last from commutativity of the union and the definition of
. If now
is symmetric and contains we have where
- the first equality follows from the definition of
; - the second inclusion from the assumption that
and from compatibility of the opposite with the order (proposition 1.49), so that ; - the third equality from the fact that
is symmetric; - the last from idempotency of union.
Thus,
is the symmetric closure of . Assume is reflexive. Then where:
- the first inclusion follows from the assumption that
is reflexive; - the second from the definition of union;
- the last from the definition of
. Thus,
is reflexive if is.
- Clearly
. Also, is transitive because where:
- the first equality follows from the definition of
; - the second from formula:
; - the third from the definition of powers of a relation;
- the fourth from idempotence of the union;
- the last from the definition of
. If now
is transitive, then where:
- the first implication follows from compatibility of the product with inclusions (proposition 1.49);
- the second from the fact that
by transitivity of ; - the third from the definition of union;
- the last from the definition of
. This proves that
is the transitive closure of . Assume is reflexive, i.e. that . Then is reflexive because where:
- the first inclusion follows by the assumption;
- the second by the definition of union;
- the last from the definition of
. Assume
is symmetric, i.e. . Then is symmetric because where:
- the first equality follows from the definition of
; - the second from the compatibility of the opposite with unions (proposition 1.50);
- the third from compatibility of the opposite with products (proposition 1.51);
- the fourth from the assumption that
is symmetric; - the last from the definition of
.
Induced Order
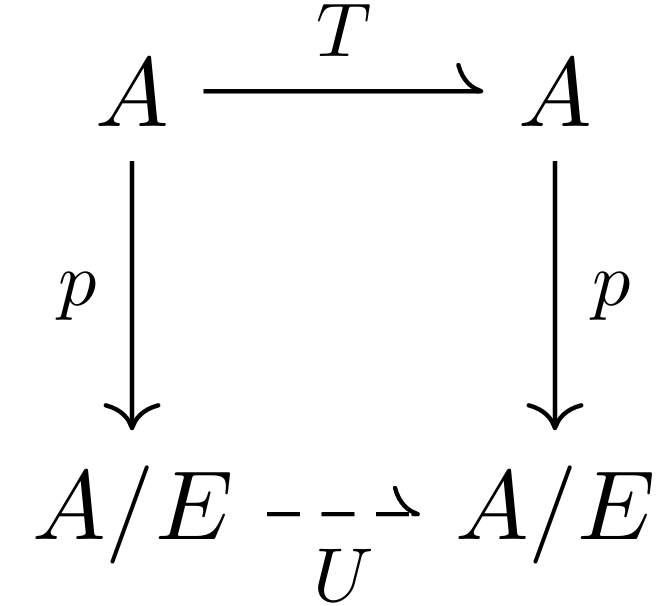
Theorem 1.122: Induced Order
Let
be a binary relation and let be its reflexive and transitive closure. Then the relation is an equivalence relation on and if is the projection on the quotient, the direct image of
along is a partial order on , called the partial order induced by . If is antisymmetric and is therefore the generated order, then is isomorphic to .
Proof
We refer to the diagram below.
is an equivalence relation.
For reflexivity observe that
where:
- the first equality follows from idempotency of intersection;
- the second from compatibility of the opposite with the multiplicative structure;
- the third from the fact that
because is reflexive, therefore by compatibility of the opposite with inclusions and finally from the compatibility of products with inclusions; - the last equality from the definition of
. Thus
and is reflexive. To prove symmetry observe that
where:
- the first equality follows from the definition of
; - the second from compatibility of opposites with intersections;
- the third from the involution property of opposites;
- the fourth from commutativity of intersections;
- the last from the definition of
. To prove transitivity observe that
where:
the first equality follows from the definition of
; the second inclusion from compatibility of orders with intersections (
and ); the third inclusion from properties of the intersection;
the fourth from the fact that
because is both reflexive and transitive and therefore by compatibility of opposites with products and inclusions; the last from the definition of
.
- We let
and prove that is a partial order. Observe first that . The first equality follows from the inclusions where:
- the first equality follows from the fact that the identity is neutral for the product;
- the second inequality from the fact that
and from compatibility of the product with inclusion; - the third from the fact that
and again compatibility of the product with inclusion; - the last equality from reflexivity and transitivity of
. The second formula is proved similarly, inverting the order of
and . We prove that
: where:
- the first equality follows from the definition of
; - the second from the fact that
; - the third from the fact that
; - the last from the definition of
. To prove that it is both reflexive and antisymmetric we show that
. Suppose is a binary relation on . Then where:
- the first equivalence follows from the properties of intersections;
- the second from the definition of
; - the third from multiplication by
on the left and on the right and the fact that in one direction, and from multiplication by on the left and by on the right in the other direction; - the fourth from the fact that
and therefore ; - the fifth equivalence follows from properties of the intersection;
- the sixth from the fact that
; - the last from multiplication by
on the left and on the right and the fact that in one direction and from multiplication by on the left and on the right in the other direction. Thus,
and 1 have the same subsets and are therefore equal.
- Assume now that
is antisymmetric. Since it is also reflexive, , so that is injective; However, is always surjective and therefore it is an isomorphism from to .
Epi Factorization Lemma
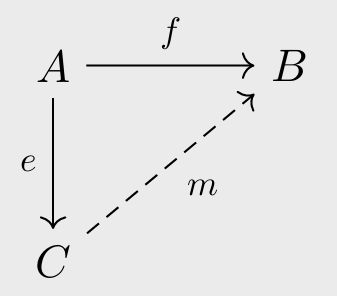
Lemma 1.144: Epi Factorization Lemma
Assume, in the diagram below, that
is an arbitrary function and is an epimorphism.
Then
factors through if and only if . In this case for a unique ; moreover
Proof
- Assume a factorization
exists. Then where:
- the first equality follows from the definition of kernel pair;
- the second from the fact that the identity is neutral for the product;
- the third inclusion from the fact that
because is a function (proposition 1.59); - the fourth equality from compatibility of the opposite with products;
- the fifth from the fact that (
) is a factorization of ; - the last from the definition of kernel pair.
Also observe that we must have
where:
- the first equality follows from the fact that
is neutral for the product; - the second from the fact that
because is an epimorphism (proposition 1.72); - the third from the assumption that
. Thus, if a factorization exists it must be unique.
- Assume
. In this case the relation provides a factorization of via ; in fact where:
- the first equality follows from the fact that
is neutral for the product; - the second inclusion from the fact that
because is a function (proposition 1.59) and from compatibility of the product with inclusion; - the third inclusion from the hypothesis that
and again from compatibility of the product with inclusion; - the fourth from the fact that
because is a function (proposition 1.59) and from compatibility of product and inclusion; - the last equality from the fact that
is neutral for the product. This shown that
and thus that the relation factors via . It remains to prove that
is a function. First, where:
- the first equality follows from the definition of
; - the second from compatibility of the opposite with products;
- the third from the fact that the opposite is involutory;
- the fourth from the assumption that
; - the fifth from the fact that
is a function; - the last from the fact that the identity is neutral for the product.
Moreover,
where:
- the first equality follows from the definition of
; - the second from compatibility of the opposite with products;
- the third from the fact that the opposite is involutory;
- the fourth from the fact that
because is a function; - the fifth from the fact that the identity is neutral for the product;
- the last from the fact that
is an epimorphism. Observe that the formula also proves that the kernel pair of
is the direct image along of the kernel pair of . As to , observe that since is surjective we have and therefore where:
- the first equality follows from the definition of equality;
- the second from the fact that
is surjective; - the third from the definition of product function;
- the fourth from the fact that
; - the last from the definition of image of
.
Chapter 2
Consistency posets are contained in finitary ones
Proposition 2.112
Every consistency poset is contained in a finitary one.
Proof
Declare that
if for every finite subset we can find such that .
- We prove that
is a consistency poset.
Suppose
is a variable and . If then is finite and therefore , contradicting the fact that is a consistency poset. Thus . If
and is either or , then . For otherwise , and since is finite we would have , contradicting the fact that is a consistency poset. Double negation. Suppose
. If is finite, then where is a finite subset of containing . But then and since is a consistency poset, . Thus, and since is an arbitrary finite subset of we have . Suppose
. If is finite, then where is a finite subset of containing . Therefore, and since is a consistency poset, . But then and therefore . Suppose
. If , there exist two finite subsets , for which are not contained in any element of . Observe that , for otherwise , being a finite subset of , would be contained in an element of . Now observe that there exists a finite subset such that and . Since is finite, there exists such that and since and is a consistency poset, for some index . But then against the assumption.
- To see that
, observe that given any , every finite subset is contained in and therefore by definition of . - We prove that
is finitary. Suppose and is finite. Every finite subset is also a finite subset of and therefore for some ; thus (note that finiteness of does not play any role here). Conversely, suppose for every finite subset . Since is a finite subset of itself, and .
Compactness
Theorem 2.115: Compactness
A set of formulas
is satisfiable if and only if every finite subset of is.
Proof
Necessity is clear, for if a valuation satisfies
, it also satisfies is every subset of , finite or not. For sufficiency, define a subposet
by stipulating that if and only if every finite subset of is satisfiable. We prove that is a consistency poset.
- Assume
and . Since is finite and unsatisfiable, it can not be a subset of . Thus . - Assume
. Since both sets and are finite and unsatisfiable, they can not be subsets of . Therefore . - Suppose
. If is finite, then there exists a finite subset containing such that . Since is a finite subset of and is satisfiable, say by a valuation . Since , we have ; therefore and and hence . Since every finite subset is satisfiable, . - Suppose
. If is finite, there exists a finite subset containing such that . Since is finite and is satisfiable, say by a valuation . Since and therefore . Thus and therefore . Since this is true for all finite , we have . - Suppose
. If neither nor there exist finite subsets such that is unsatisfiable for ; we can also assume that for both indices. But then is satisfiable, being a finite subset of , say . Since , we have . Therefore for at least one index and therefore , a contradiction. Since
is a consistency poset, every is satisfiable (corollary 2.114). Since every finite subset of is satisfiable, we have and therefore is satisfiable.
Consistency implies satisfiability for regular inferences
Proposition 2.145
For a completely regular inference relation every consistent set is satisfiable.
Proof
Assume
is consistent. By the Lindenbaum lemma,
is contained in a complete consistent set ; if we prove that is is satisfiable, then so is . Thus, it suffices to prove that every complete consistent set is satisfiable. Define a valuation
setting . We prove that the set
coincides with
and we do this by structural induction with uniform notation. Observe first that
; in fact, assuming , by completeness of we have and therefore
. We now use structural induction.
- Atomic case. By the above remark, it suffices to prove that
for every atomic . If is a propositional variable, then by definition of . If , then by consistency of and , hence . If , then by the truth axiom and therefore (proposition 2.143); on the other hand, , so that . - Double negation. This follows from the initial remark applied twice: if
then and therefore . - Conjunctive formulas. Suppose
and . By proposition 2.143 and the semantics of conjunctive formulas we have and therefore
. 4. Disjunctive formulas. Assume and . By completeness of and properties of valuations we have and therefore
. From proposition 2.145 and theorem 2.135, we finally have
Corollary 2.146: Every completely regular inference is complete.
Consistency poset of a regular inference
Proposition 2.149
For a regular inference, the class
of consistent sets is a consistency poset.
Proof
We verify that the conditions in the definition of consistency class are satisfied.
- If
then (corollary 2.137). Thus if , then . - If
then by assumption; thus, if . Also, if then by assumption; by the truth rule and therefore (corollary 2.137); thus . - Double negation. Assume
. The proof below shows that if , then is inconsistent. Therefore, if , then .
Step Claim Reason 1 hypothesis 2 hypothesis 3 1, assumption 4 formula (2.313) 5 3,4, cut 6 5,2, cut
-formulas. Assume . The derivation on the left below shows that if , then is inconsistent. Therefore, if , then .
Step Claim Reason Step Claim Reason 1 hypothesis 1 hypothesis 2 hypothesis 2 hypothesis 3 1, assumption 3 hypothesis 4 3, (2.340) 4 1, assumption 5 4, 2, cut 5 2, 3, (2.341) 6 3, (2.340) 6 4,5 cut 7 6, 5, cut
-formulas. Assume . The derivation on the right above shows that if for , then is inconsistent. Therefore, if , then for at least one . We therefore have an alternative way of proving completeness for an inference relation:
Corollary 2.150
Every regular inference relation is complete.
is a regular inference, the the class of consistent sets is a consistency poset (proposition 2.149). Therefore, every consistent set is satisfiable (proposition 2.114) and the inference is complete (theorem 2.135). If