4.2 - View- and Conflict-Serializability

---

View-Serializability

View-serializability is a crucial concept in database concurrency control, ensuring that the execution of concurrent transactions produces results that are consistent with some serial execution of those transactions. To understand view-serializability, we first need to establish some preliminary definitions.

Definitions

1. Read-From Relationship: In a schedule , a read operation is said to read from a write operation if precedes in the schedule and there is no intervening write operation on between and . This relationship captures the notion of which transaction’s write a read operation is actually observing.

2. Final Write: A write operation in a schedule is considered a final write if it is the last write on object that occurs in that schedule. This concept is vital for determining the outcome of reads in the schedule.

Two schedules and are view-equivalent (denoted ) if they satisfy the following conditions:

• They contain the same operations.
• They maintain the same read-from relationships.
• They have the same final writes for each object.

A schedule is termed view-serializable if it is view-equivalent to a serial schedule involving the same transactions. The class of view-serializable schedules is denoted as .

A mnemonic to remember view-serializability is that a schedule is view-serializable if:

1. Every read operation sees the same values as in some serial execution.
2. The final value of each object is written by the same transaction that would write it in a serial order.

Example

1. Schedules and : consider the following schedules In , reads from , and also reads from . The final writes are and . Since is view-equivalent to the serial schedule , it is considered view-serializable.

2. Schedules and : consider now these other schedules In this case, reads from , and reads from . The final writes are and . Since is view-equivalent to the serial schedule , it is also view-serializable.

3. Non-View-Serializable Examples:

• Schedule :
• Schedule :
• Schedule :

These schedules demonstrate various anomalies, such as lost updates (in ), non-repeatable reads (in ), and phantom updates (in ). Each of these schedules is non-view-serializable, which can be verified by testing view equivalence with transactions and , and also with and .

More Complex Examples of View-Serializability

Let’s explore more complex schedules to illustrate the concept of view-serializability in detail.

Reads-from Relationships:

• reads from
• reads from
• reads from
• reads from

Final Writes:

• is the final write on
• is the final write on
• is the final write on

Since the reads-from relationships and the final writes align with a serial schedule, is in the view-serializable class (VSR).

Now consider another complex schedule:

Reads-from Relationships:

• reads from
• reads from
• reads from
• reads from

Final Writes:

• is the final write on
• is the final write on
• is the final write on

The schedule has the same reads-from relationships and the same final writes as a serial schedule. Thus, it is view-serializable (in VSR).

Reads-from Relationships:

• reads from
• reads from (not from )

Final Writes:

• is the final write on
• is the final write on
• is the final write on

Although the final writes in are correct, the reads-from relationships differ from the ones in the serial schedules. For example, reads from , which violates the view-equivalence condition where should have read from . Therefore, is not view-serializable and cannot be considered view-equivalent to a serial schedule like .

Complexity of View-Serializability

Determining whether two schedules are view-equivalent can be done efficiently in polynomial time and space. However, deciding if a schedule belongs to the class of view-serializable schedules (VSR) is an -complete problem. This complexity arises because it involves examining all possible serial schedules with the same operations to check their reads-from relationships and final writes. This combinatorial nature makes the process computationally intensive.

To mitigate this, a more stringent but easier-to-verify definition can be applied, even though it might exclude some schedules that would be valid under the broader view-serializability criterion.

Conflict-Serializability

In concurrency control, conflict-serializability is an essential concept to ensure that a schedule of operations results in a database state equivalent to some serial execution of transactions. The idea is to detect and manage conflicts between operations to maintain the correctness of database transactions.

Definition

Two operations and from different transactions (where ) are said to be in conflict if they operate on the same resource (data item), and at least one of the operations is a write. There are two types of conflicts:

1. Read-Write Conflict (denoted or ): This occurs when one transaction reads a resource and another transaction writes to the same resource.
2. Write-Write Conflict (denoted ): This occurs when two transactions attempt to write to the same resource.

Two schedules, and , are considered conflict-equivalent (denoted as ) if:

• They contain the same operations.
• In all pairs of conflicting operations, the order of execution is the same in both schedules.

A schedule is conflict-serializable if it is conflict-equivalent to some serial schedule involving the same transactions. In other words, the schedule can be transformed into a serial schedule by reordering non-conflicting operations without changing the result of the transaction executions. The class of conflict-serializable schedules is denoted as .

The relationship between view-serializability and conflict-serializability is expressed as follows:

this means that all conflict-serializable schedules are also view-serializable, but not all view-serializable schedules are conflict-serializable. This is because a schedule that is view-serializable may still contain conflicting operations that prevent it from being conflict-equivalent to a serial schedule.

Example

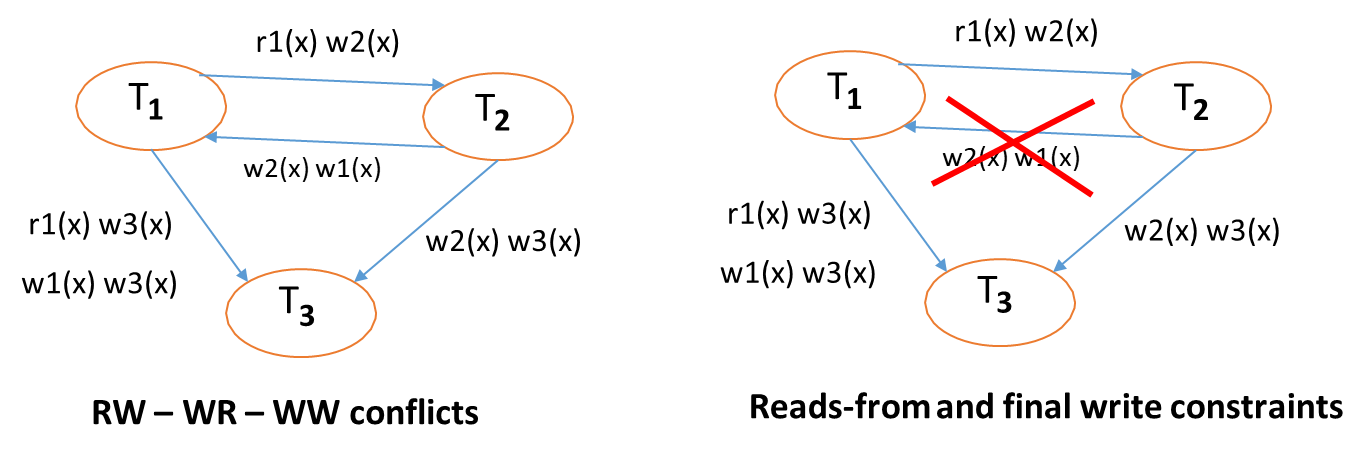
For example, consider the schedule:

• This schedule is view-serializable because it is view-equivalent to the serial schedule .
• However, it is not conflict-serializable because the conflicting operations and cannot be reordered in a way that maintains the required order in a serial schedule.

It can be proven that if two schedules are conflict-equivalent, they are also view-equivalent. Specifically, if , then .

Proof

This can be shown by verifying two conditions:

1. Same Final Writes: Both schedules must have the same final write operations on each data item. If they didn’t, there would be at least two conflicting write operations in a different order, violating conflict-equivalence.
2. Same Reads-From Relationship: Both schedules must have the same reads-from relationships, meaning that any read operation in both schedules must read the same value written by the same write operation. If the reads-from relationships differed, there would be a conflict between the operations, violating conflict-equivalence.

Thus, if , then they must have the same final writes and the same reads-from relationships, ensuring .

To further illustrate this, assume . In this case, there must be a pair of conflicting operations in a different order between and , violating conflict-equivalence. This contradiction shows that must imply .

To determine if a schedule is conflict-serializable (i.e., can be reordered into a serial schedule without changing the outcome), we can construct and analyze a conflict graph. This graph visually represents the conflicts between operations in different transactions.

Definition

A conflict graph is made of two components:

1. Nodes: Each transaction in the schedule is represented by a node.
2. Edges: An edge from transaction to is added if there is a conflict between two operations from and from , and precedes in the schedule.

Theorem

A schedule is conflict-serializable if and only if the conflict graph is acyclic.

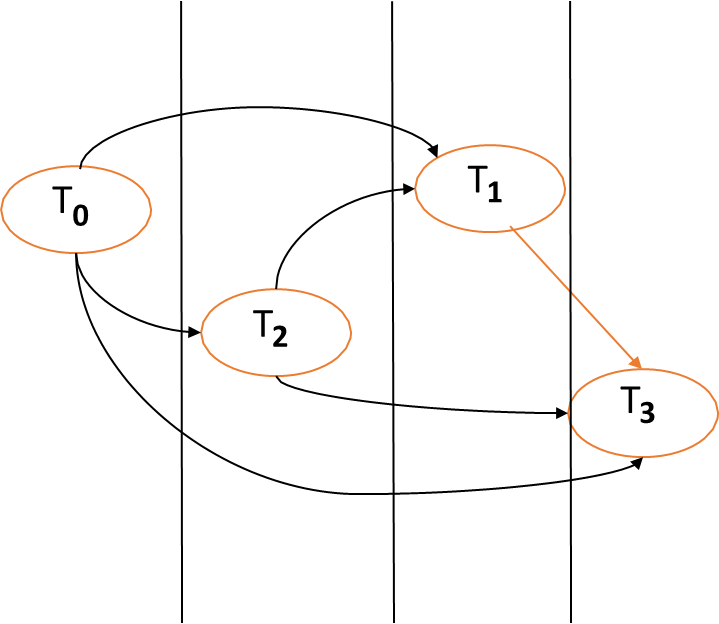
Example Schedule

Consider the schedule:

Let’s break the operations down by each resource:

resource

This helps identify the conflicts between transactions. For example:

• On resource : conflicts with .
• On resource : all conflict with one another (as they are write-write conflicts).
• On resource : conflicts with .

Using the resource projections, we construct the conflict graph based on the conflicting operations:

graph LR
  T0((T0))
  T1((T1))
  T2((T2))
  T3((T3))

  T0 --> T1 --> T3
  T0 --> T2 --> T3
  T0 --> T3
  T2 --> T1

Since the conflict graph contains no cycles, the schedule is conflict-serializable. This means there is at least one serial schedule that preserves the order of conflicting operations.

When a schedule adheres to Conflict Serializability, it inherently implies that its corresponding Conflict Graph must be acyclic. Without loss of generality, if we consider a serial schedule where transactions are ordered as , then by the very nature of conflict equivalence, all conflicting operations present in schedule must maintain the same relative order as they do in . Consequently, within the conflict graph, any arc signifies a conflict between transaction and transaction . If precedes in the equivalent serial schedule, then the arc in the conflict graph can only exist if . The presence of an arc where would indicate a conflicting pair ordered differently than in the serial schedule, which would violate the condition of conflict equivalence. Therefore, the absence of such “backward” arcs (i.e., arcs where ) inherently prevents the formation of cycles in the conflict graph, as a cycle necessitates at least one such backward arc to complete the loop.

If the conflict graph of a schedule is acyclic, it directly implies that the schedule is conflict-serializable.

An acyclic conflict graph naturally induces a topological partial ordering on its nodes, which correspond to the transactions within the schedule. This topological ordering ensures that for every arc in the graph, transaction precedes transaction in this partial order. This same partial order is then applied to the transactions of schedule . Any serial schedule constructed by ordering its transactions according to this partial order will be conflict-equivalent to . This is because, for every conflicting pair of operations , the acyclic nature of the graph guarantees that always precedes in the topological sort.

For instance, if a partial order dictates , any serial schedule respecting this order (e.g., ) will be conflict-equivalent to the original schedule.

It is important to note that an acyclic conflict graph may permit multiple compatible serial schedules, as there can be numerous total orderings that are consistent with a given partial topological order.

The number of such compatible serial schedules is equivalent to the total number of linear extensions of the partial order defined by the acyclic conflict graph.

Example

Going back to the previous example, considering the schedule

we have the following conflict graphs: