4 - Logic

---

Mathematical logic serves as a foundational formalism that is particularly valuable for its descriptive capabilities. Logic is often regarded as a “universal” language due to its close alignment with natural language, making it accessible and applicable across a broad spectrum of disciplines beyond just computer science. This universality enables the formulation of precise arguments and reasoning structures, facilitating clear communication of complex ideas.

In the realm of theoretical computer science, mathematical logic has numerous connections and applications. Various notations and languages used in programming and specification often draw upon logical principles, allowing for a robust framework in which software can be designed, analyzed, and verified. For instance, many programming languages incorporate logical constructs to enable clear expression of conditions and flow control, which is essential for writing efficient and error-free code.

Furthermore, mathematical logic intertwines with several key areas in computer science, including automata theory, formal languages, and grammars. These connections reveal how logic can be used to understand and model computational processes.

For example, automata can be characterized using logical expressions, and the study of formal languages often involves the application of logical frameworks to determine the properties and behaviors of different language classes.

Several significant results in the field of logic have profound implications for computer science, particularly regarding expressive power and the decidability of various logical problems. The expressive power of a logic refers to its ability to capture different kinds of information and reasoning, which can impact how effectively a language can represent algorithms and systems. Additionally, questions related to the decidability of the satisfiability and validity problems explore whether certain logical statements can be systematically resolved, thereby influencing the complexity of decision procedures used in computational contexts.

Logical Connectors Summary

Logical Connector	Symbol / Abbreviation	Meaning / Definition
Negation		”Not ”; true if is false
Conjunction		”And”; true if both and are true
Disjunction		”Or”; true if at least one of , is true
Implication		”If then ”; equivalent to
Universal Quantification		”For all , holds”; equivalent to
Existential Quantification		”There exists such that holds”
Equality		” equals ”; defined as

Monadic First Order Logic (MFO)

The Monadic First-Order Logic (MFO) is a simplified first-order logic adapted to describe languages over an alphabet . This logic provides a powerful formalism for characterizing word properties, using monadic predicates and a restricted set of logical operators. MFO enables the definition of language properties without needing to use second-order logic, which can be computationally more complex.

Formula

The basic syntax of MFO allows for the expression of predicates over individual symbols in a word. The primary form of formulas in MFO is as follows:

where, denotes a predicate associated with a character in the alphabet . Each character is assigned its own predicate , which is monadic because it involves only one argument, (position). This predicate is true if the character at position in a word matches . The relation represents the usual “less-than” relation over positions in a word, allowing us to compare positions of characters.

Variables in MFO range over a finite set of natural numbers , where each number represents a character’s position within a word of length . This range is useful for indexing each character in the string sequentially, making MFO a convenient logic for working with word structures.

Useful Abbreviations and Standard Abbreviations in MFO

Several logical operators are defined using standard abbreviations to simplify expressions:

• Conjunction: is defined as .

• Implication: is represented by .

• Universal Quantification: is expressed as .

• Equality: is defined by .

• Less-than-or-equal: is given by .

• The constant is represented as .

• The concept of a successor, indicating the next position, is defined by:

  This definition captures that immediately follows , a useful tool for defining consecutive character relationships. Constants like , etc., can be defined as successors of , etc., respectively, allowing for the definition of specific positions in a word.

• In the same way, we define the predecessor relation as: This captures the idea that immediately precedes , allowing us to express relationships between characters in a word in both forward and backward directions.

• Symbol: To denote the last position in the word, we use the expression , defined as , indicating that there is no index greater than .

• Symbol: The first position in the word is denoted by , defined as , meaning there is no index less than .

Examples of Logical Formulas

1. Words Where the Symbol is : This can be expressed as:

   This formula asserts that there exists an index such that is the last position in the word and the symbol at that position is .

2. Words Where the Third-last Symbol is : To specify that the third-last symbol of a word is (assuming the word has at least three symbols), we can use:

   This formula indicates that there exists an index such that the symbol at is , and there exists an index that is two positions after , which is also the position in the word. This can be abbreviated further as:

Interpretation of Words in MFO

In the context of MFO, we define the interpretation of logical formulas based on the structure of words over an alphabet .

Definition

A word, or string, denoted by , belongs to the set , which consists of all possible strings formed using the symbols from the alphabet .

For any symbol , the predicate is interpreted such that it holds true if and only if the symbol at position in the word is .

The first symbol in the word is indexed at position 0.

Example

For example, the formula

is satisfied if the word starts with the symbol (it can be directly translated as there exists a position at the beginning of a word that is an ). In this case, the existential quantifier is stating that there exists an index (specifically, ) such that the predicate is true, meaning that the first character of is .

Another logical formula that can be expressed is one that requires every occurrence of the symbol to be immediately followed by the symbol . This can be formalized as follows:

This formula asserts that for every index where holds, there must exist an index such that is the successor of (i.e., ), and the symbol at this position must be .

Semantics of MFO

The semantics of MFO provides a formal framework for interpreting the logical expressions defined within this logic.

Let be a word belonging to the set of strings , where is an alphabet. The set represents all the variables that can be used within MFO formulas.

Definition

An assignment, denoted as , is a function that maps each variable in to a position within the string .

Specifically, the range of is defined as , where denotes the length of the string .

The semantics of MFO can be articulated through various interpretation rules:

1. Interpretation of Predicate : The expression holds true if the symbol at position in the word matches the predicate . In other words, and , indicating that the ^th symbol of is .

2. Comparison of Positions: The statement is true if the position of is less than the position of , specifically .

3. Negation: The expression is valid if it is not the case that . This indicates that does not hold for the given assignment and word.

4. Disjunction: The semantics for disjunction is satisfied if at least one of the formulas or holds under the assignment . Thus, or must be true.

5. Existential Quantification: For the existential quantification , this holds if the length of the word and there exists an index such that the modified assignment makes true. The notation denotes the assignment that assigns the value to the variable while keeping other assignments unchanged.

Language of Closed Formulas

The language associated with a closed formula (or sentence) is defined as . This means that comprises all words over the alphabet that satisfy the formula .

It is noteworthy that the empty string does not satisfy any existential quantifications.

This characteristic implies that the empty string can only fulfill universal quantifications, thereby affecting how we interpret logical formulas that include existential variables. In practical terms, this limitation must be taken into account when constructing formulas that could potentially include the empty string, ensuring that they adhere to the rules of MFO while accurately reflecting the properties of the language being defined.

Properties of MFO

Monadic First-Order Logic exhibits several important properties that govern the languages it can define.

One of the key characteristics of MFO is its closure properties. Specifically, all languages definable by MFO are closed under the operations of union, intersection, and complement. This means that if you have two languages defined by MFO, you can create new languages through these operations, and they will also be definable within MFO.

For instance, we can combine formulas using logical connectives such as conjunction, disjunction, and negation.

Example

1. The formula asserts the existence of a character that is the last symbol of a word, and another that occurs two positions before the last.

2. The formula indicates that either there is a last character that is or there is an that is immediately followed by the last character.

3. The negation states that there is no position in the word where is the last symbol.

While MFO is robust in defining languages through the aforementioned operations, it is important to note that MFO is not closed with respect to the Kleene star operator (). The Kleene star allows for the representation of languages through repetitions of strings, but MFO cannot express all such languages.

Property

A significant property of MFO is that every language defined over a one-letter alphabet (for example, ) can be expressed in MFO if and only if it is finite or co-finite (the complement of a finite language).

For example, the formula defines the finite language .

However, when we attempt to define the language (the Kleene star of ), this language is neither finite nor co-finite, highlighting the limitation of MFO in capturing all regular languages.

MFO is specifically adept at defining what are known as regular star-free languages. These are languages that can be expressed through the operations of union, intersection, complement, and concatenation of finite languages without the use of the Kleene star. As a result, MFO defines a subset of regular languages.

Example

For example, the language can be considered star-free even though its expression includes the Kleene star; it can still be represented in MFO through logical expressions. Moreover, the language , which encompasses all strings composed of the symbols and , can be expressed as the complement of the empty set.

Therefore, while can be denoted without the star in MFO, it remains an important example of how MFO operates within the bounds of regular languages.

In MFO, the expression and related formulations encapsulate the characteristics of star-free languages, reinforcing the logic’s ability to succinctly define patterns within words. Furthermore, MFO allows for statements such as , emphasizing the logical structure that underpins the definition of languages without utilizing the Kleene star.

Monadic Second-Order Logic (MSO)

Monadic Second-Order Logic (MSO) expands upon Monadic First-Order Logic (MFO) by allowing quantification not only over individual positions in a word but also over sets of positions. This enhancement is crucial for defining all regular languages. In MFO, quantification is limited to positions, represented by natural numbers. In contrast, MSO introduces the capability to quantify over monadic predicates, effectively allowing the representation of sets defined by such predicates.

In MSO, we utilize monadic predicates to define sets of positions.

Definition

A monadic predicate is a unary predicate that can be interpreted as a property that certain positions may satisfy.

Thus, if holds true, it signifies that position is included in the set represented by . Consequently, MSO includes formulae such as , where is a variable ranging over monadic predicates.

For clarity, we use capital letters to denote variables over monadic predicates and lowercase letters for variables that represent positions.

MSO Semantics

The semantics of MSO builds upon the semantics established in MFO by incorporating a new type of variable, which quantifies over sets of positions. The assignment for these second-order variables (denoted as ) is defined as a function:

This means that each variable in is assigned a subset of positions within the word .

The additional semantics introduced for MSO are as follows:

• The statement holds true if and only if the position is an element of the set defined by the monadic predicate as assigned by .
• The expression is satisfied if there exists a subset such that , where indicates that the variable is assigned the set .

Example Formula for Regular Language

Using MSO, we can formulate expressions for specific regular languages. For example, consider the language . We can represent this language with the following MSO formula:

In this formula:

• is a monadic predicate used to identify odd positions in the string. This means that is true for positions that are classified as “odd.”
• The formula asserts that:
  • The first position (0) is not included in .
  • The predicate alternates as we move along the word (odd positions are marked as such).
  • The symbol at position must be .
  • If is the last position in the word, then it must belong to the set defined by .

Shorthand Notation in MSO

In MSO, we often use shorthand notation to simplify the representation of logical formulas. This notation allows us to express complex relationships and properties more concisely.

• : this is true if and only if is the first position in :
• :
• : this is true if and only if is the following position of in :
• : this is true if and only if is the previous position of in :
• : this is true if and only if is the subset of made by the first, third, fifth, etc. positions of :

• : this is true if and only if is the subset of made by the second, fourth, sixth, etc. positions of :
• : this is true if and only if the cardinality of is odd:
• : this is true if and only if the cardinality of is even:

From Finite State Automata to MSO

Finite State Automata can be effectively represented using Monadic Second-Order Logic through the use of second-order quantifications. This is particularly useful because MSO allows us to express properties of the states of the automaton via predicates.

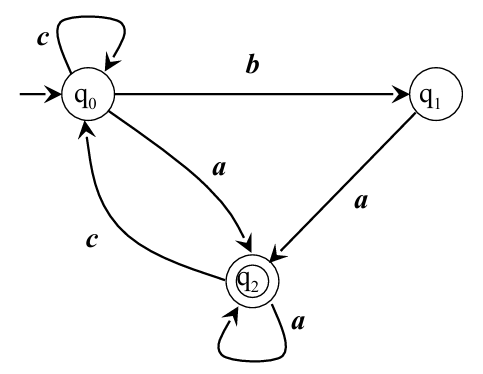
Consider an FSA defined by three states , , and . The MSO formula representing this automaton can be expressed as follows:

1. Existential Quantification of States: The formula begins with , indicating that we are introducing predicates that represent the states of the automaton.
2. State Exclusivity: The first part, , ensures that no position can belong to more than one state at a time. This enforces that the states are mutually exclusive.
3. Initial State: The condition states that the automaton starts in state at position 0.
4. Transition Conditions: The main body of the formula includes transitions for the automaton:
   • The formula captures the transition rules for states based on the input symbols , , and .
   • Each transition is expressed in terms of the current state and the character read at position .
   • For example, denotes that if the automaton is in state at position and reads an , it transitions to state at position .
5. Handling Position: The formula also considers the last position in the input word with the conditions related to . If is the last position, it ensures that the automaton ends in one of the valid accepting states, as specified by the transitions.

From MSO to FSA

The relationship between MSO and FSA is captured by the Büchi-Elgot-Trakhtenbrot Theorem, which asserts that

any language definable by an MSO formula can be recognized by a finite state automaton.

This means that the class of languages definable by MSO exactly coincides with the class of regular languages.

MSO is expressive enough to capture all regular languages through its ability to quantify over sets of positions (using second-order variables), allowing for complex properties of sequences to be described. Conversely, any regular language defined by an FSA can also be expressed in MSO, since the behavior of the automaton can be characterized by its states and transitions, which can be represented using monadic predicates and logical quantifications.

Steps

1. Identify Predicates: Determine the predicates in the MSO formula that correspond to different states and transitions in the automaton.
2. Define States: Each unique configuration represented in the MSO formula corresponds to a state in the FSA. The states should reflect the conditions that need to be satisfied by the words accepted by the automaton.
3. Establish Transitions: For each logical expression in the MSO formula that represents a transition (such as moving from one state to another upon reading a specific symbol), create corresponding transitions in the FSA.
4. Initial and Accepting States: Identify the initial state (based on the structure of the formula) and the accepting states (where the conditions defined by the MSO formula are satisfied).