4.2 - Adversarial Search Strategies – Monte Carlo Tree Search

---

Classical adversarial search algorithms, such as Minimax and its essential optimization, Alpha-Beta Pruning, form a robust theoretical basis for creating Artificial Intelligence agents in deterministic, two-player, zero-sum games. These foundational techniques operate by exhaustively or quasi-exhaustively exploring the game state space. However, their practical application in games with vast state spaces and deep game trees reveals two principal inherent limitations concerning evaluation and search strategy.

1. Reliance on an Evaluation Function: In games where the search depth cannot feasibly reach terminal states (e.g., deep-play games like Chess), these algorithms must truncate their search at a predetermined depth. At this horizon depth, a static evaluation function is indispensable for assigning a heuristic, non-terminal value to the current game state. The efficacy of the AI player is thus critically dependent on the quality of this function. Creating a good evaluation function requires deep domain knowledge and is often more of an art than a science.
2. Uniform Search Strategy: Alpha-Beta pruning explores the game tree in a fixed, depth-first manner. While the algorithm achieves significant pruning by identifying and discarding branches that are provably suboptimal (i.e., those that will not influence the final Minimax value), it fundamentally explores the remaining unpruned game tree in a fixed depth-first manner. Crucially, it lacks an intrinsic mechanism to dynamically prioritize or allocate computational resources based on the promise or likelihood of success of a particular move. Essentially, all unpruned branches are treated with the same investigative effort, leading to potentially inefficient exploration by not focusing the search on the most strategically salient areas of the game tree.

Case Study: The Game of Go

The ancient game of Go stands as a paradigmatic example where the limitations of classical Minimax and Alpha-Beta Pruning are severely exposed, necessitating the development of a completely new approach to adversarial search. The game’s complexity is driven by several critical factors.

1. Enormous Branching Factor: Go exhibits an enormous branching factor, averaging around possible moves per turn, which starkly contrasts with Chess’s average of approximately . This massive exponential growth of the search tree renders a deep, brute-force lookahead computationally infeasible within reasonable time constraints.
2. Long Game Length: Go is characterized by an exceptionally long game length, frequently exceeding moves. This prolonged temporal horizon means that strategic consequences of a move can take an extensive number of turns to materialize, demanding an unprecedented search depth to fully appreciate the move’s ultimate impact.
3. Lack of a Good Evaluation Function: Go presents an extreme challenge in developing an effective static evaluation function. The value of an intermediate board position is highly subtle, global, and holistic, dependent on the complex interplay of territory, influence, and life-and-death groups. Local tactical evaluations often fail to capture the board’s true strategic landscape. Furthermore, seemingly insignificant variations in board layout can translate to drastically divergent final outcomes, underscoring the inadequacy of simple heuristic functions.

Monte Carlo Tree Search (MCTS)

Monte Carlo Tree Search (MCTS) represents a powerful, heuristic approach to adversarial search, successfully overcoming the critical limitations associated with classical algorithms like Alpha-Beta Pruning. This methodology was pivotal to the success of advanced AI agents like AlphaGo and is now considered the state-of-the-art technique for decision-making in numerous complex games. MCTS is fundamentally defined by the integration of two core concepts: evaluation by statistical rollouts and asymmetric, selective search.

Evaluation and Selective Search Dynamics

Instead of relying on a human-engineered, static evaluation function to estimate the value of non-terminal game states, MCTS employs a method of statistical estimation. This process, known as evaluation by rollouts (or playouts), involves simulating a large number of complete games from a given state to a terminal outcome. The overall win, loss, and draw rates derived from these thousands of simulated games provide a statistically robust, empirical estimate of the position’s true value. The core insight is that even when using a fast, simple (often random) default policy for the rollouts, a genuinely superior game position will, on average, yield a higher proportion of favorable outcomes compared to an inferior one. As the quantity of simulations is increased, the statistical estimate converges toward greater accuracy, thereby obviating the need for complex, handcrafted heuristics.

Furthermore, MCTS implements a selective search strategy, which contrasts sharply with the uniform, depth-first exploration characteristic of Alpha-Beta Pruning. The algorithm incrementally and asymmetrically constructs its search tree, dynamically prioritizing the computational resources dedicated to branches that appear most promising based on the gathered rollout statistics.

Steps

The simplest way to understand MCTS is to consider how it evaluates the available moves from a given position. The algorithm performs the following for each possible move:

1. Make the move.
2. From the resulting position, play a large number of games to the end using a simple, fast policy (e.g., random moves). These are the “rollouts.”
3. Count the number of wins, losses, and ties.
4. The move with the highest win percentage is considered the best.

Example

Consider the simplified version of Tic-Tac-Toe: from an initial board state, MCTS explores three possible moves. For each move, it runs 10,000 simulations.

• Move 1: Leads to a win rate for player X.
• Move 2: Leads to a win rate for player X.
• Move 3: Leads to a win rate for player X.

Based on this statistical evidence, Move 1 is the most promising choice. The key insight is that even with random playouts, a truly superior position will, on average, lead to more wins than an inferior one. As the number of simulations increases, this statistical estimate becomes more accurate.

The Four-Phase MCTS Iterative Cycle

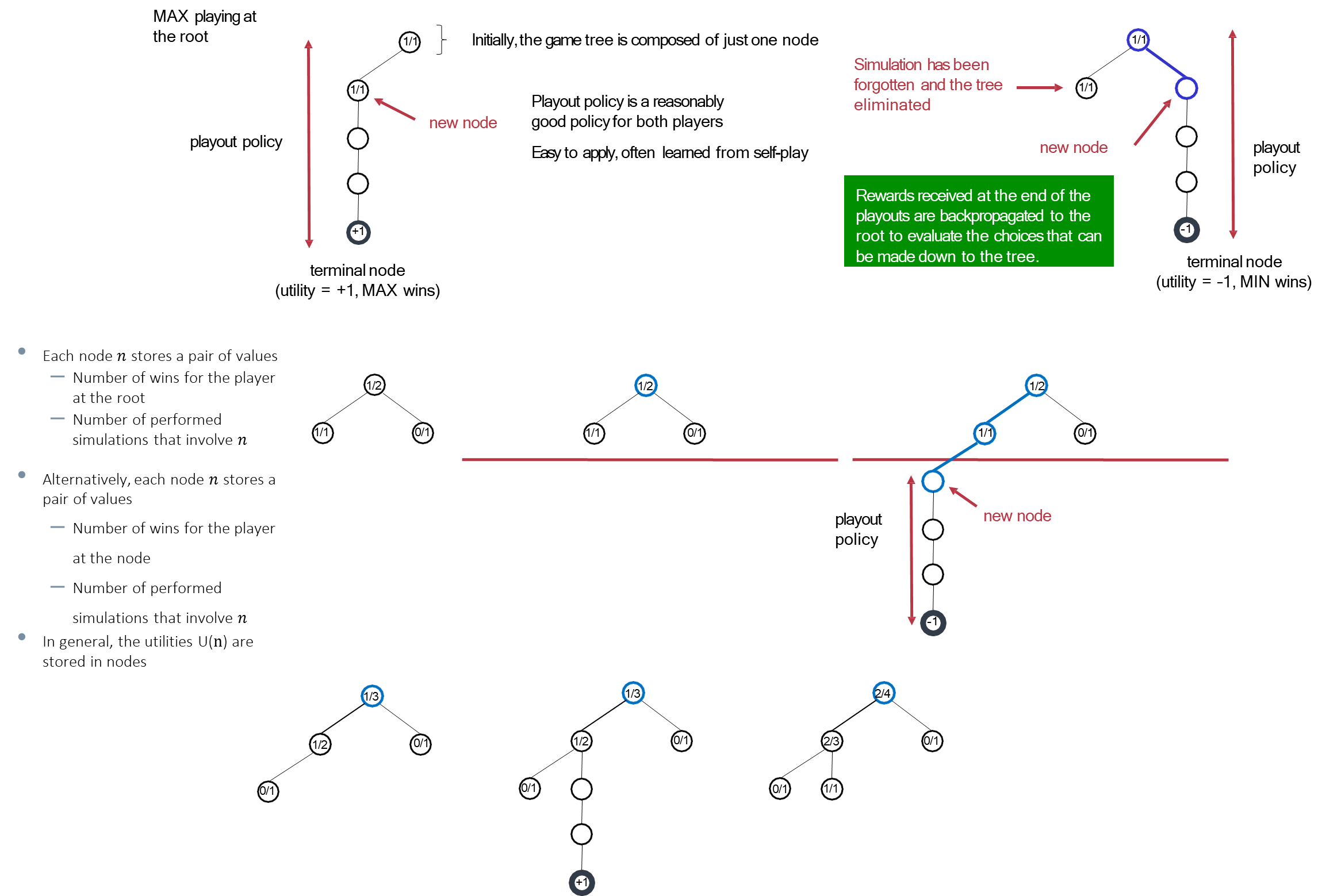
MCTS operates as an anytime algorithm, meaning it can be interrupted at any point to yield the current best move, with solution quality monotonically improving with time and iterations. Its operational core is an iterative four-phase cycle: Selection, Expansion, Simulation, and Backpropagation.

1. Selection: The cycle begins at the root node (the current game state). The algorithm then traverses the existing tree structure down to a leaf node—a node not yet fully explored. This traversal is governed by a tree policy, which must skillfully balance the need for exploration (investigating new or under-sampled game states) and exploitation (deepening the search in paths already proven to be highly successful). A common mathematical implementation of this policy is the Upper Confidence Bound 1 applied to Trees (UCT) formula.
2. Expansion: Upon reaching the selected leaf node, if it does not represent a terminal game state, the tree is expanded. This involves adding one or more child nodes to the tree, corresponding to valid, unexplored moves from the current position.
3. Simulation (Rollout): From one of these newly expanded nodes, a single, complete game is played out to a terminal state. This is the rollout phase, executed using a pre-defined, typically fast default policy (e.g., a simple random move generator or a slightly more informed heuristic). The eventual outcome of this simulation (win, loss, or draw) is recorded.
4. Backpropagation (Update): The recorded result of the simulation is then propagated backward up the search tree along the path from the expanded node to the root. At every node along this path, two critical statistics are updated: the total number of visits (simulations that passed through the node) and the total number of wins recorded from those simulations. Specifically, a win increments both statistics for all nodes on the path, while a loss only increments the visit count.

This continuous cycle gradually builds an asymmetric search tree where the nodes corresponding to promising lines of play acquire a significantly higher density of both visits and accumulated reward. The final move decision is based on the most-visited child of the root node. This move is deemed the most statistically robust choice, as it represents the action that has been subjected to the most intense investigation and consistently contributed to successful game outcomes within the search process.

Algorithm

The iterative nature of the algorithm is captured in the following pseudocode:

function MONTE-CARLO-TREE-SEARCH(state) returns an action
  tree ← NODE(state)
  
  while IS-TIME-REMAINING() do
    leaf ← SELECT(tree)
    child ← EXPAND(leaf)
    result ← SIMULATE(child)
    BACK-PROPAGATE(result, child)
  
  return the move in ACTIONS(state) whose node has highest number of playouts

The final decision is made by selecting the move corresponding to the child of the root node that was visited the most times. This is considered the most robust choice, as it’s the move that has been most thoroughly investigated and consistently found to be part of promising lines of play.

The Exploration-Exploitation Dilemma

The most critical and nuanced part of MCTS is the Selection phase. How does the algorithm decide which path to take down the tree? This decision is governed by the need to solve the classic Exploration-Exploitation Dilemma.

• Exploitation: The algorithm should focus on the moves that have proven to be successful in previous simulations (i.e., have a high win rate). This is exploiting current knowledge to win.
• Exploration: The algorithm must also try moves that have been visited less frequently. A move with a lower win rate might simply be underexplored; with more simulations, it could prove to be the best move. This is exploring to improve knowledge.

If the algorithm only exploits, it might settle on a suboptimal move early on and never discover a better one. If it only explores, it wastes time on obviously bad moves. A successful MCTS implementation must balance these two competing needs.

The statistics gathered from rollouts are inherently uncertain, especially when the number of simulations for a given node is low.

A move that shows a 70% win rate after 100 simulations is likely more reliable than a move showing a 50% win rate after just 10 simulations.

The selection policy must account for this uncertainty. This challenge is the central topic of the Multi-Armed Bandit problem, and solutions like the UCT (Upper Confidence bounds applied to Trees) algorithm are used to mathematically balance exploration and exploitation during the selection phase.

The Multi-Armed Bandit (MAB) Problem

The critical challenge of balancing exploration and exploitation within the Selection phase of the Monte Carlo Tree Search (MCTS) algorithm is elegantly framed and solved by borrowing principles from a classic reinforcement learning problem: the Multi-Armed Bandit (MAB) Problem. This problem provides a robust mathematical framework for optimizing sequential decision-making under uncertainty, which perfectly models the process of choosing the most promising child node to search next.

The k-Armed Bandit Analogy for MCTS

The -Armed Bandit scenario conceptualizes an agent facing a row of distinct slot machines (“one-armed bandits”), each possessing an independent and unknown probability distribution for dispensing a reward. The agent’s objective is to determine a sequence of pulls, spanning a total budget of rounds, that maximizes the cumulative reward

In the context of MCTS, this analogy maps directly to the tree structure:

• Each child node of the current node in the search tree is analogous to a single slot machine.
• The act of running a simulation (pull) through that child node yields a reward (the win/loss/draw outcome).
• The total number of MCTS iterations remaining serves as the total time budget .

The fundamental dilemma remains:

an agent must decide whether to exploit a child node that has historically shown a high win rate (high estimated reward), or to explore a child node that has been infrequently visited to gather more definitive information about its true potential.

Exploitation risks missing out on a superior, but yet unproven, move, while excessive exploration risks wasting valuable computational budget on demonstrably inferior branches. A principled solution must allocate the finite simulation budget (the pulls) to the child nodes (the machines) in a way that minimizes cumulative regret and converges efficiently to identifying the optimal move.

Real-World Significance

Formally, the MAB problem dictates that at each discrete time step , the agent selects an action at​ from the set of available actions and consequently observes a stochastic reward . The overarching goal is the maximization of the expected total reward over a predefined horizon . This framework is not merely a theoretical construct but has profound practical utility, particularly in fields where sequential decision-making under limited information is crucial.

Example

A salient real-world example is found in Randomized Clinical Trials.

A physician testing different treatments for a disease faces an identical exploration-exploitation trade-off. If Treatment 1 shows initial promise, the doctor is tempted to exploit this knowledge by assigning it to all incoming patients. However, doing so would prematurely curtail the collection of crucial, high-variance data on Treatments 2 and 3 (exploration), potentially preventing the discovery of a superior long-term cure.

The optimal MAB strategy, such as one implemented by the Upper Confidence Bound (UCB) algorithm, provides the mathematical mechanism necessary to dynamically and intelligently assign patients to treatments, thereby balancing the ethical mandate of providing the currently best-known treatment with the scientific imperative of gathering sufficient data to definitively determine the true optimal treatment for the population. This systematic balancing mechanism is precisely what the MCTS tree policy requires to select the most promising path down the game tree.

Action Value Estimation and the Upper Confidence Bound Principle

The effective implementation of the Multi-Armed Bandit (MAB) framework in the MCTS Selection phase necessitates a robust method for estimating the expected value of each potential move (action) and a principled strategy for addressing the inherent uncertainty in these estimates.

Estimating Action Values via Sample Averages

The theoretical true value of an action , denoted , is defined as the expected mean reward received upon selecting that action, formally expressed as . Since this true mean is unknown in a stochastic environment, we rely on the sample-average method for estimation. The estimated value of action at time , , is calculated as the arithmetic mean of all rewards accrued from selecting that action up to time :

To maintain computational efficiency, especially in the context of thousands of MCTS iterations, this calculation is typically performed using an incremental update formula. After receiving the ^th reward ​ for action , the new estimate ​ can be calculated without storing all historical rewards:

This formula effectively moves the old estimate () towards the new evidence (), weighted by the learning rate , which is typically set to , that is, the reciprocal of the number of times action has been selected.

The UCB Principle

The most successful and mathematically rigorous methods for solving the MAB problem are founded upon the principle of “Optimism in the Face of Uncertainty.” This strategy recognizes that the current sample average estimate, , is subject to uncertainty, and the true value is likely to lie within a statistical confidence interval around . The width of this interval is directly related to the number of times the action has been sampled; fewer samples imply greater uncertainty and a wider interval.

The optimistic approach dictates that, for decision-making purposes, we should select actions based on their potential to be the best, not just their current average performance. This potential is quantified by the Upper Confidence Bound (UCB) of the action’s estimated value.

Consider three actions, , , and . While action might possess the highest average reward , if action has been sampled significantly less, its uncertainty component will be large, resulting in a wide confidence interval and, consequently, the highest UCB. The optimistic strategy will therefore select .

This choice systematically resolves the exploration-exploitation dilemma:

• Exploitation is promoted because actions with high average rewards (high ) will naturally have high UCBs.
• Exploration is inherently encouraged because actions that are less explored will possess a large uncertainty bonus, artificially inflating their UCB and prioritizing them for investigation.

UCB Action Selection in MCTS

The principle of “Optimism in the Face of Uncertainty” is mathematically formalized and implemented within MCTS through the Upper Confidence Bound (UCB) action selection algorithm, specifically the UCB1 variant. This strategy defines the tree policy for the Selection phase, dictating which child node to descend into at each step of the MCTS iteration. At every time step , the algorithm selects the action at​ that maximizes the sum of its estimated average value and an exploration bonus, as expressed by the fundamental UCB formula:

The UCB selection criterion is a composite score that ensures computational focus is intelligently allocated across the search tree:

1. Exploitation Term (): This is the sample-average reward for action . It represents the greedy component of the policy, directly favoring moves that have historically resulted in high win rates during previous simulations. A high indicates a high observed performance and encourages the algorithm to exploit this known successful path.

2. Exploration Term (): This term is the confidence interval bonus that quantifies the uncertainty surrounding the estimate . Its primary role is to promote exploration by artificially inflating the score of under-sampled actions.

   • (Visits of action ): As the denominator, this is the most critical component. When an action has been selected a small number of times ( is small), the entire exploration term becomes large, giving a significant temporary boost to the action’s overall UCB score. This ensures that even actions with a mediocre current average reward are eventually given a chance to be thoroughly investigated, preventing the algorithm from prematurely discarding potentially optimal, yet under-explored, moves.
   • (Total Visits): The total number of simulations run across all child nodes. The inclusion of ensures that the exploration pressure slowly increases as the overall simulation count grows, a necessary feature to guarantee that every action is sampled an asymptotically infinite number of times, thus satisfying theoretical convergence properties.
   • (Exploration Constant): A tunable, user-defined parameter () that explicitly scales the magnitude of the exploration bonus. A higher value of promotes a more risk-taking, exploratory search strategy, whereas a lower value prioritizes exploitation of currently known high-value nodes.

Example

The power of the ​factor is clearly demonstrated through computational examples. Let’s assume total simulations have run and we are calculating the exploration bonus:

• If an action was tried times:
• If an action was tried times:
• If an action was tried times:
• If an action was tried only times:

This significant difference ensures that the algorithm’s attention is intelligently diverted towards the less-charted but potentially more rewarding regions of the search space.

The UCB formula thus provides a theoretically robust and computationally efficient means of performing optimal allocation of search effort. By selecting the action that maximizes this combined score, MCTS efficiently balances the need to refine the value estimates of moves known to be good (exploitation) with the necessity of investigating moves whose true value is highly uncertain (exploration). This principle is the key algorithmic driver behind the superior performance of MCTS in games with vast and complex search spaces.

Applying UCB to Monte Carlo Tree Search

The Upper Confidence Bound (UCB) algorithm, derived from the Multi-Armed Bandit problem, is directly integrated into the Selection phase of MCTS, giving rise to the UCT (Upper Confidence bounds applied to Trees) algorithm. UCT serves as the tree policy, guiding the search from the root node down to an unexplored leaf by iteratively selecting the child node that maximizes its UCB value. This process ensures an optimal, dynamic balance between exploring new game states and exploiting known successful lines of play.

UCB1

The UCB1 for trees formula, applied at any given node to select its next child, is defined as:

The formula separates the decision criterion into distinct components that serve the exploration and exploitation objectives:

Component	Formula	Description	Role in Search
Exploitation Term		The sample mean reward (or win rate) for the current player at node . - : utility of node (number of wins) - : number of simulations involving	This term favors nodes with a high historical success rate, driving the search to exploit previously successful game lines. is the total utility (wins/reward) and is the total visit count.
Exploration Term		The uncertainty bonus, or exploration pressure. - : exploration parameter - : number of simulations involving the parent of node	This term actively encourages the selection of nodes that have been less explored relative to the total search effort directed toward their parent, thereby promoting exploration.

The exploration parameter allows for tuning the search’s aggressiveness: setting to zero results in a purely greedy, exploitative search, while a high promotes a wider, more exploratory search. The repeated selection of the child node maximizing this UCT value ensures that the MCTS algorithm progressively refines the estimates of the most promising moves.

MCTS Iteration with UCT Guidance

A single MCTS iteration, guided by UCT, proceeds through the standard four phases.

1. Selection (UCT-Guided): Starting at the root, the UCT value is calculated for all immediate children. The child node with the maximal UCT score is selected. This process recursively repeats down the tree. For instance, if the root has children and , and , the algorithm descends to . This continues until a node is reached that is either unexpanded or fully expanded but still meets the UCT criterion for exploration.
2. Expansion, Simulation, and Backpropagation: Once the selection policy leads to a leaf node that is not a terminal state, a new child is added (Expansion). A Simulation (rollout) is then performed from this new node to the end of the game, yielding a terminal result (e.g., loss or utility of ). Finally, the result is propagated up the entire path back to the root (Backpropagation). The visit count of every node on this path is incremented by 1, and the utility is updated based on the rollout’s outcome. This incremental update effectively incorporates the new statistical evidence into the tree structure, preparing the statistics for the next UCT-guided selection phase.

Algorithmic Advantages of MCTS

The integration of UCT and rollouts provides MCTS with significant architectural and functional advantages over deterministic, evaluation-function-dependent methods like Alpha-Beta Pruning:

• Elimination of the Explicit Evaluation Function: MCTS’s most transformative feature is its non-reliance on a handcrafted static evaluation function. The value of any game state is learned dynamically and statistically through the observed outcomes of thousands of random rollouts. This self-learning approach makes MCTS uniquely suitable for games like Go, where designing a heuristic function is intractable, and allows it to be applied to novel domains without requiring extensive prior domain expertise.
• Asymmetric and Selective Tree Growth: The UCT policy enables the algorithm to strategically allocate its limited computational resources. The resulting search tree is asymmetric and sparse, dedicating search depth and width disproportionately to game lines that have been identified as most promising, while pruning the exploration of demonstrably inferior branches. This adaptive focusing dramatically enhances search efficiency in games with colossal branching factors.
• Anytime Algorithm Property: MCTS is inherently an anytime algorithm, a crucial feature for competitive environments with strict time controls. It can be interrupted at any moment and will return the move corresponding to the child of the root with the best current statistical probability, ensuring that the quality of the solution scales predictably and monotonically with the time allocated.

Comparison - Minimax, Alpha-Beta Pruning, random player

Given the context of deterministic, perfect-information games like Tic-Tac-Toe and the nature of the algorithms—Minimax, Alpha-Beta Pruning, and a random player—we can make precise predictions about the expected outcomes of playing games.

Minimax vs. Random Player (Tic-Tac-Toe)

Minimax is a complete algorithm for small, finite, deterministic games like Tic-Tac-Toe. When allowed to search to the full depth of the game tree, Minimax will play a perfect game, meaning it will select a move that leads to the best possible outcome (win, then draw, then loss).

Since Tic-Tac-Toe is a solved game with the optimal outcome being a draw if both players play perfectly, the Minimax player will aim for a win if possible, or a draw otherwise. Against a purely random player who makes arbitrary moves, the Minimax player will be able to capitalize on almost every mistake.

• Prediction: The Minimax player will win the vast majority of games, possibly nearly all of them, with a few draws occurring if the random player happens to make a sequence of suboptimal moves that still avoid an immediate loss. The random player is highly unlikely to win a single game.
• Result: Minimax dominates the random player (near 100% win rate for Minimax).

Minimax vs. Minimax (Tic-Tac-Toe)

When two Minimax players, both searching to the full depth, play against each other, both are playing an optimal strategy. Since Tic-Tac-Toe’s optimal outcome for perfect play is a draw, neither player will be able to force a win against the other’s best defense.

• Prediction: Every single game will result in a draw.
• Result: All games will be a draw (0% win rate for both).

Minimax vs. Alpha-Beta Pruning (Tic-Tac-Toe)

Alpha-Beta Pruning is an optimization of the Minimax algorithm. It generates the exact same final move as Minimax; it just does so significantly faster by avoiding the exploration of branches that are guaranteed not to affect the final Minimax value.

Since both algorithms are mathematically guaranteed to produce the optimal move, they are strategically equivalent in terms of game outcome.

• Prediction: The games will result in the same outcomes as two Minimax players, but Alpha-Beta Pruning will run faster computationally.
• Result: All games will be a draw (0% win rate for both).

Two Minimax Players (Breakthrough)

Breakthrough is a modern abstract strategy game that, unlike Tic-Tac-Toe, has a very large state space and is generally considered computationally intractable to solve completely. It is an asymmetric game where the optimal strategy is not a draw; the game is suspected to be a win for the first player (White), but this has not been mathematically proven.

When two Minimax players play, they are playing the best move they can find within their search depth. Since they cannot search to the end of the game (the tree is too deep), they must rely on a heuristic evaluation function at the search horizon.

• Prediction: The outcome will be determined entirely by the quality and symmetry of the heuristic evaluation function used by the two players. If the heuristic is flawed or favors one side slightly, that player will win most games. If the heuristic is very good and approximately symmetric, the outcome will likely favor the player who has the theoretical win advantage (White/First Player), but the games will be won and lost, not necessarily drawn.
• Result: The outcome is undetermined but likely non-draw, and heavily dependent on the quality of the heuristic function and the search depth. Assuming the game is a first-player win, the first Minimax player will likely win more often.

Alpha-Beta Pruning vs. MCTS (Tic-Tac-Toe)

This match pits a complete search algorithm (Alpha-Beta, which plays perfectly) against a stochastic, anytime search algorithm (MCTS).

• Alpha-Beta Pruning will play perfectly, guaranteeing a draw or better.
• MCTS relies on simulation and statistical estimates. Given enough time (iterations), MCTS will also converge to near-perfect play.

Since the optimal outcome in Tic-Tac-Toe is a draw, and Alpha-Beta Pruning guarantees perfect play, MCTS will not be able to force a win. As long as MCTS has enough time to run enough simulations (high ) to converge to the optimal move, it will also play perfectly.

• Prediction: If MCTS is allowed sufficient time for each move, both players will play perfectly.
• Result: All games will be a draw. If MCTS is constrained by a very short time limit, its imperfect play might occasionally allow Alpha-Beta to win (e.g., if MCTS fails to block an immediate win), but this is unlikely in a simple game like Tic-Tac-Toe.

A Synthesis of AI Game-Playing Strategies

The development of an Artificial Intelligence agent for game-playing can be systematically categorized into distinct philosophical approaches. Each strategy represents a trade-off between the need for domain-specific knowledge and the desire for algorithmic generality. For simple games like Tic-Tac-Toe, all methods can yield a strong player, but their scalability and applicability differ drastically for complex games.

The Expert System Approach (Handcrafted Rules)

This approach leverages a developer’s deep understanding of a game to encode a rigid set of rules or heuristics—an expert system. The player’s decisions are based on a prioritized series of if-then-else statements that mirror human tactical thinking.

Example

For Tic-Tac-Toe, this involves immediate winning moves, followed by defensive blocks, and finally heuristic positional moves (e.g., taking the center or a corner).

The significant limitation is the method’s lack of generality and inherent brittleness. A slight variation in rules (e.g., transitioning from Tic-Tac-Toe to the -in-a-row game Gomoku) necessitates a complete re-engineering of the rule set, as optimal strategies are not easily transferable. Furthermore, the system’s performance is entirely dependent on the human developer’s proficiency and is prone to unforeseen gaps or edge cases that can cause the player to fail in non-trivial situations.

The Classical Search Approach (Minimax & Alpha-Beta Pruning)

The classical approach is centered on provable optimality through extensive lookahead. Algorithms like Minimax and the optimized Alpha-Beta Pruning define the game structure (legal moves, terminal states) but rely on the search process itself, rather than explicit rules, to determine the optimal move.

Pros	Cons
General Strategy: The search algorithm is game-agnostic and can be applied to any deterministic, two-player, zero-sum game.	Computational Complexity: Exponential time complexity makes full search infeasible for games with high branching factors (e.g., Chess, Go).
Optimal: Given enough time, it will find the provably best move.	Requires an Evaluation Function: Practical use requires search cut-off and an evaluation function for non-terminal states, reintroducing the need for domain-specific knowledge.
No Proficiency Needed: The developer only needs to implement the game’s mechanics, not its strategy.

For games like Chess, the vast search tree necessitates a cut-off at a shallow depth, which, in turn, requires a handcrafted evaluation function to score non-terminal positions. This requirement undermines the initial generality, reintroducing the need for significant domain-specific expertise.

The Statistical Search Approach (Monte Carlo Tree Search - MCTS)

MCTS represents a paradigm shift from exhaustive search to statistical sampling and selective search. It evaluates game states not by a static function, but by simulating thousands of games (rollouts) from that state to completion, using the outcome probabilities as the value estimate.

Pros	Cons
No evaluation function needed: bypasses the need for a handcrafted evaluation function, making it suitable for games where one is hard to design.	Expensive simulations: simulations are computationally expensive, especially for complex games requiring many or lengthy simulations.
General: the core algorithm is game-agnostic, similar to Minimax.	Potentially uninformative: if the default (rollout) policy is purely random, simulations may not provide enough meaningful information to distinguish between subtly different but important moves, especially early in the game.

The Modern Synthesis: AlphaZero and Self-Learning Agents

The limitations of classical and statistical search methods—the need for handcrafted heuristics or the inefficiency of purely random rollouts—are resolved by the Modern Synthesis approach, exemplified by AlphaZero. This approach combines the power of deep learning with the strategic depth of Monte Carlo Tree Search (MCTS) within a Reinforcement Learning (RL) framework. AlphaZero learns to play a game entirely from a tabula rasa state, utilizing only the rules of the game and achieving superhuman performance through iterative self-play.

At the core of the AlphaZero system is a single, deep convolutional neural network (often referred to as a residual network) parameterized by and denoted . This network serves a dual purpose, acting as both the learned evaluation function and the learned policy function.

The network accepts the raw representation of the current board state, , as its input (including a limited history of preceding moves to capture critical game-specific dynamics like the rule in Go or the three-fold repetition rule in Chess). It produces a two-headed output vector:

1. Policy Vector (): A probability distribution over all legal moves from state . This is the network’s —its immediate, learned estimate of the strategic merit of each move.
2. Value (): A single scalar output, typically constrained between (loss) and (win). This is the network’s , providing an instantaneous, probabilistic assessment of the final game outcome from the current state.

This relationship is concisely described as .

The Self-Reinforcing Training Loop

AlphaZero’s learning occurs through a continuous, self-reinforcing training loop that generates increasingly higher-quality data and uses it to iteratively improve the neural network. This cycle establishes a “virtuous cycle” of policy and value improvement.

Self-Play and Data Generation

In this phase, the current best version of the neural network plays games against itself. A crucial distinction is made during move selection: the agent does not simply choose the move suggested by the raw policy output . Instead, at each state :

• An MCTS search is conducted, but it is deeply informed by the neural network. The network’s policy is used to bias the exploration towards moves the network already suspects are good, and its value is used to efficiently encountered during the search. This network-enhanced MCTS is vastly more efficient and intelligent than MCTS with random rollouts.
• The MCTS search, by combining the network’s intuition with deep lookahead, produces a search-enhanced policy, . This resulting policy is a much stronger, search-refined probability distribution over moves than the network’s raw policy ; MCTS acts as a .
• The move is chosen by sampling from .
• Upon game completion, the final binary outcome (win , loss , draw ) is recorded. Each turn generates a training sample .

Neural Network Training

The collected self-play data is utilized in a Supervised Learning step to train a new version of the network . The training objective is to minimize a loss function that has two principal components:

• Policy Head Loss: This term measures the difference (using cross-entropy loss) between the network’s raw policy output and the superior, search-refined target policy . The network is effectively trained to mimic the output of its own MCTS search, absorbing the search depth into its immediate intuition.
• Value Head Loss: This term measures the difference (using mean-squared error loss) between the network’s value output and the actual final game outcome . The network is trained to accurately predict the final result from any given intermediate position, creating a highly refined, data-driven evaluation function.

This newly trained network, , replaces the old one if it demonstrates superior performance, and the entire self-play and training cycle repeats. The iterative refinement allows AlphaZero to rapidly acquire, memorize, and leverage strategic patterns, making it the definitive approach for achieving super-human skill in complex zero-sum games.