Definition
Computing performance is the total effectiveness of a computer system in terms of throughput, response time, and availability. It can be characterized by the amount of useful work accomplished by a computer system or computer network compared to the time and resources used.
It is common practice to validate systems primarily against functional requirements rather than versus quality one is essential. Although, little information related to quality is typically available early in the system lifecycle, such understanding is crucial from both cost and performance standpoints. This importance extends to the design and system sizing phases, as well as to system evolution in response to changes in workloads or the number of users.
The system can be evaluated by using:
- Intuition and trend extrapolation: this is rapid and flexible but lacks accuracy. It also requires highly skilled personnel to be effective.
- Experimental evaluation of alternatives: this is expensive and laborious, but it yields accurate knowledge of system behavior under one set of assumptions. Experimentation is always valuable, often required, and sometimes the approach of choice. A further drawback: an experiment is likely to yield accurate knowledge of system behavior under one set of assumptions, but not any insight that would allow generalization.
To analyze the system quality, we generally use models that are:
an attempt to distill, from the details of the system, exactly those aspects that are essential to the system behavior. - E. Lazoswka
Models are used to drive design decisions, such as which architecture to use, how many resources to meet some performance/reliability goal, etc. Often models are the only artifact to deal with, especially during the design phase. There are two main types of techniques to evaluate system quality:
- Measurement-based:
- Direct measurement: measuring the system directly.
- Benchmarking: comparing the system with other systems.
- Prototype: building a prototype of the system.
- Model-based:
- Analytical and numerical: based on the application of mathematical techniques, which usually exploit results coming from the theory of probability and stochastic process. They are the most efficient and the most precise, but are available only in very limited cases.
- Simulation: based on the reproduction of traces of the model. They are the most general, but might also be the less accurate, especially when considering cases in which rare events can occur. The solution time can also become really large when high accuracy is desired.
- Hybrid techniques: combine analytical/numerical methods with simulation.
flowchart TB 1[Techniques] --- 2[Measurement-based] 2 --- 3[Direct measurement] 2 --- 4[Benchmarking] 2 --- 5[Prototype] 1 --- 6[Model-based] 6 --- 7[Analytical and numerical] 6 --- 8[Simulation] 6 --- 9[Hybrid techniques]
Queueing Theory
Definition
Queueing theory is the theory behind what happens when you have a lot of jobs, scarce resources, and so long queue and delays.
Queueing network modelling is a particular approach to computer system modelling in which the computer system is represented as a network of queues. A network of queues is a collection of service centers, which represent system resources, and customers, which represent users or transactions. Queueing theory applies whenever queues come up. Queues in computer systems are:
- CPU that uses a time-sharing scheduler.
- Disk that serves a queue of requests waiting to read or write blocks.
- A router in a network that serves a queue of packets waiting to be routed.
- Databases that have lock queues, where transactions wait to acquire the lock on a record.
Predicting performance (e.g., for capacity planning purposes), is built on an area of mathematics called stochastic modelling and analysis.
A queueing network is successful when the low-level server details of a system are largely irrelevant to its high-level performance characteristics.

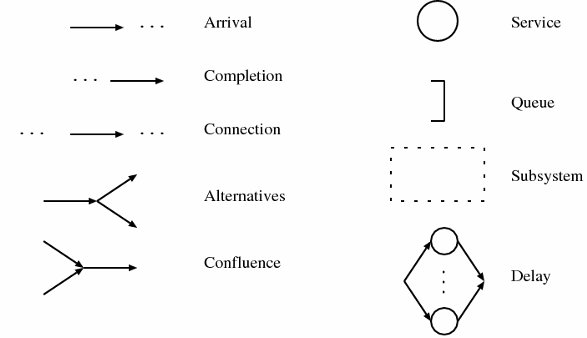
The queueing network can be represented as a graph where we have:
- The arrivals to the queue represented as an arrow directed to the server
- A service center composed of:
- The queue
- The server
- The departures from the queue represented as an arrow directed out the server
Arrival
Definition
Arrivals represent jobs entering the system: they specify how fast, how often, and which types of jobs does the station service.
Arrival can come from an external source or another queue, or even from the same queue through a loop-back arc.
Service center
Definition
Service represents the time a job spends being served.
In the service center, we can have different numbers of servers:
- Single server: capability to serve one customer at a time. The waiting customers remain in the buffer until chosen for service. The next customer is chosen depending on the service discipline.
- Infinite server: there are always at least as many servers as there are customers, each customer can have a dedicated server. There is no queueing (and no buffer) in such facilities.
- Multiple servers: fixed number of
servers, each of which can service a customer at any time. If the number of customers in the facility is less than or equal to , there will be no queueing. If there are more than customers, the additional customers will have to wait in the buffer.
Queue
Definition
The queue represents the buffer where jobs wait to be served.
If jobs exceed the capacity of parallel processing of the system, they are forced to wait in a queue or in a buffer. When the job currently in service leaves the system, one of the jobs in the queue can enter the now free service center. The service discipline/queuing policy determines which of the jobs in the queue will be selected to start its service.
Population
Definition
The population is the total number of customers in the system.
Ideally, members of the population are indistinguishable from each other. When the members of the population are not indistinguishable, we divide the population into classes whose members all exhibit the same behavior. Different classes differ in one or more characteristics, for example, arrival rate, service demand. Identifying different classes is a workload characterization task.
Queueing Networks
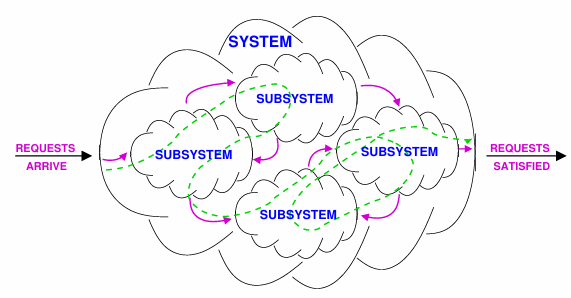
For many systems, we can adopt a view of the system as a collection of resources and devices with customers or jobs circulating between them. We can associate a service center with each resource in the system and then route customers among the service centers. After service at one service center, a customer may progress to other service centers, following some previously defined pattern of behavior corresponding to the customer’s requirement.
The queueing network can be represented as a graph where nodes represent the service centers and arcs the possible transitions of users from one service center to another. Nodes and arcs together define the network topology.
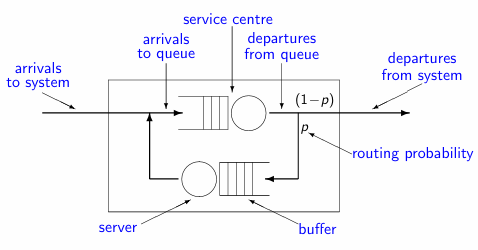
A queueing network can be open, closed, or mixed:
- Open: customers may arrive from, or depart to, some external environment. A typical example is a web server.
- Closed: a fixed population of customers remains within the system. A typical example is a client-server system with a finite number of customers.
- Mixed: there are classes of customers within the system exhibiting open and closed patterns of behavior respectively.
The level of detail in the queueing network can vary depending on the system.
Example
A web server can be represented as a single node or as a more detailed system with multiple nodes representing different components of the server. Increasing the level of detail can provide more accurate results, but also increases the complexity of the model.
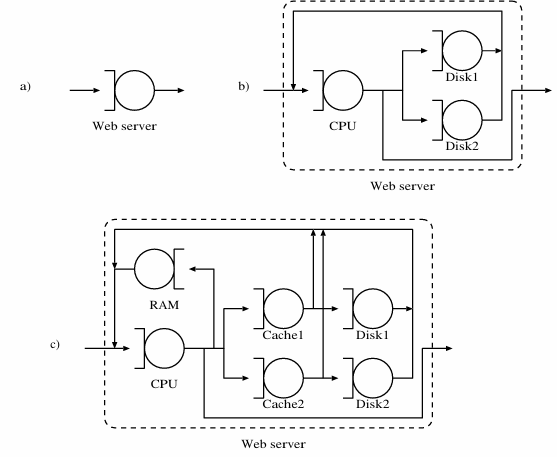
Routing
Definition
Routing is the process of selecting the path for a job after finishing service at a station.
Whenever a job, after finishing service at a station, has several possible alternative routes, an appropriate selection policy must be defined. The routing specification is required only in all the points where jobs exiting a station can have more than one destination. There are different routing algorithms:
- Probabilistic: each path has assigned a probability of being chosen by the job that left the considered station.
- Round-robin: the destination chosen by the job rotates among all the possible exits.
- Join the shortest queue: jobs can query the queue length of the possible destinations and choose to move to the one with the smallest number of jobs waiting to be served.