Reliability
Definition
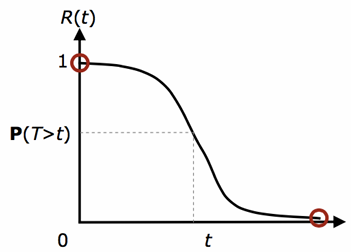
Reliability is the ability of a system or component to perform its required functions under stated conditions for a specified period of time. The Reliability of a system is the probability
that the system will operate correctly in a specified operating environment until time (assuming it was operating at time ).
If a system needs to work for slots of 10 hours at the time, then 10 hours is the reliability target. Reliability is often used to characterize systems in which even small periods of incorrect behavior are unacceptable, like in the impossibility to repair.
The probability density function of the failure is
We define also the unreliability of the system as
The exploitation of the
Info
We consider only a reliability with an exponential distribution, where the failure rate
of the system is constant over time.
We will use several terms to describe the reliability of a system:
Definitions
- Fault: is a condition that causes a system to fail in performing its required function.
- Error: is the difference between a computed, observed, or measured value and the true, specified, or theoretically correct value.
- Failure: is the event of a system or component not performing a required function according to its specifications.
Usually there is a consequence that leads to a failure, starting from a fault that causes an error that leads to a failure. However, it’s not always the case, as a fault can be non-activated, or an error can be non-propagated.
Availability
Definition
Availability is the degree to which a system or component is operational and accessible when required for use. The availability is defined as the ratio of the uptime to the sum of the uptime and the downtime; it’s also the ratio of the Mean Time To Failure (MTTF) to the sum of the MTTF and the Mean Time To Repair (MTTR).
The availability of a system is the probability
that the system will be operational at time .
It’s fundamentally different from the reliability, as the reliability is the probability that the system will not break down, while the availability is the probability that the system will be working even if it breaks down. The availability is literally the readiness for service and admits the possibility of brief outages. When the system is not repairable the availability is equal to the reliability
We can define the unavailability of the system/component as
Numbers
The availability can be expressed as a function of the “number of 9’s” and it is a fundamental number to understand the availability of a system.
| Number of 9’s | Availability | Downtime (mins/year) | Downtime/year | System |
|---|---|---|---|---|
| 1 | 90% | 52596.00 | ~5 weeks | |
| 2 | 99% | 5259.60 | ~4 days | Generic website |
| 3 | 99.9% | 525.96 | ~9 hours | Amazon.com |
| 4 | 99.99% | 52.60 | ~1 hour | Enterprise server |
| 5 | 99.999% | 5.26 | ~5 minutes | Telephone system |
| 6 | 99.9999% | 0.53 | ~30 seconds | Network switches |
| 7 | 99.99999% | 0.05 | ~3 seconds |
MTTF and MTBF
Reliability and availability are related indices because, if a system is unavailable, it is not delivering the specified system services and, therefore, it’s not making money or providing the expected service. It is possible to have systems with low reliability that must be available, as system failures can be repaired quickly and do not damage data, low reliability may not be a problem. The opposite (high reliability and low availability) is generally more difficult.
Definitions
The Mean Time To Failure (MTTF) is the mean time before any failure will occur. It’s defined as the expected value of the time to failure.
The Mean Time Between Failures (MTBF) is the mean time between two failures. It’s defined as the expected value of the time between two failures.
is another way of reporting the MTBF, as the number of expected failures per one billion hours ( ) of operation for a device.
Other indices
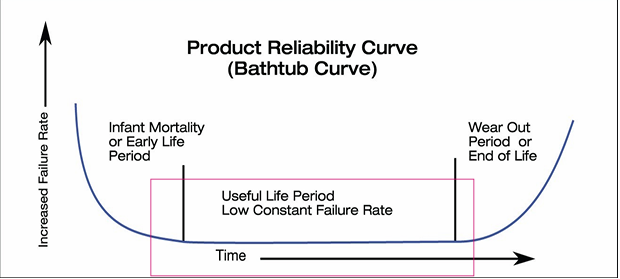
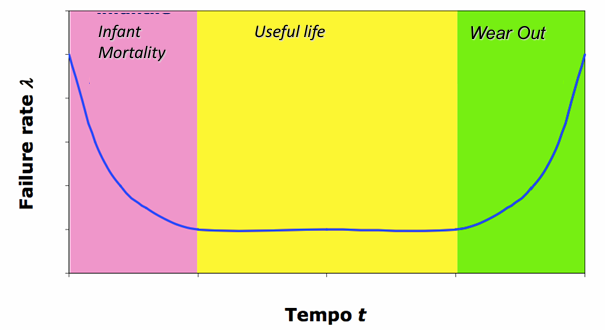
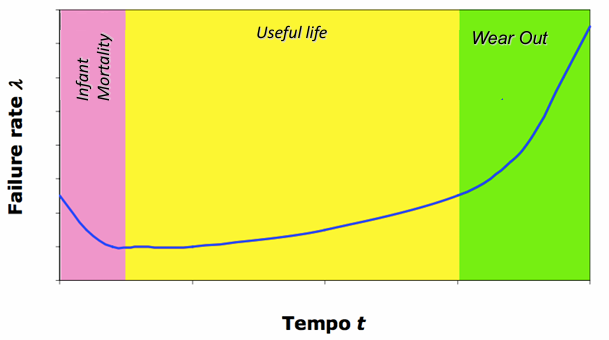
Any system’s lifetime can be divided into three phases:
- Infant Mortality: failures showing up in new systems. Usually, this period of time is present during the testing phases, and not during production phases.
- Random Failures: showing up randomly during the entire life of a system. This is the main focus of the reliability.
- Wear Out: at the end of its life, some components can cause the failure of a system. Predictive maintenance can reduce the number of this type of failures.
To measure the reliability of a system and compute the MTTF, we can use the burn-in test, a test that stresses the system with excessive temperature, voltage, current, and humidity to accelerate wear out. This process is used to identify defective products, but it’s not always reliable because it can stress the system too much and it may require a lot of time.
An empirical evaluation of the reliability can be done by considering
NOTE
The function
is the empirical function of reliability that as converges to the value .
There are many different types of faults that can occur in a system, that can be divided into two main categories: hardware faults (electronic and mechanical) and software faults.
An hardware electronic fault have a balanced distribution of the failures over time, with an infant mortality phase, a useful life, and a wear-out phase. The probability density function of the failure is a bell-shaped curve, where the infant mortality phase and the wear-out phase are balanced, while the useful life is the longest and the phase with the lowest number of failures.
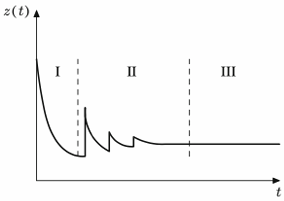
A mechanical fault has a similar distribution, but the infant mortality phase is very short and the wear-out phase is longer. The probability density function of the failure in the infant mortality phase is very low, and increases in the useful life phase, while it explodes in the wear-out phase.
A software fault has a different distribution, with an infant mortality phase and a useful life phase, but no wear-out phase, because the software doesn’t wear out; however, the update process can introduce new faults and the shape of the