Attention
No matter what NLP application we are working on, if building a search engine on documents from a web crawl, or training a phishing detector on emails from a company, we need to preprocess the text data to a format suitable for the application.
Extracting Plain Text
Text data comes in many forms, and we may need to extract text from:
- Textual documents such as
.txt, HTML, and emails are commonly processed by discarding markup (HTML tags) and other format-specific commands. In web crawl scenarios, the parser should be able to handle poorly formatted HTML. - Binary documents like Word and PDF are more complex to handle. For PDF documents, the text structure needs to be reconstructed. If the text contains multiple columns, they need to be identified to ensure the correct flow of text. If all PDFs have the same format, manual rules can be written, but machine learning may be required for varying formats.
- Images of scanned documents require specialized Optical Character Recognition (OCR) software, which is now based on deep learning. However, OCR is not perfect and may introduce recognition errors in the extracted text.
Text inside the document could be encoded in many different ways. Various text encodings could be used, which support different numbers of possible characters:
- ASCII encoding (traditional keyboard): ‘A’ → 65, ‘B’ → 66, …, ‘a’ → 97, ‘b’ → 98, …; can only display 128 characters in total.
- UTF-8 encoding (Unicode): handles 149k Unicode characters and works for over 160 languages. Unicode is needed to handle languages with non-latin character sets (e.g., Arabic, Cyrillic, Greek, Devanagari, etc.) and special characters (e.g., diacritical signs in Italian “Questa è così” and even in English: “Naïve”).
Tokenizing Text
Many (if not all) NLP tasks require tokenization, which is the process of splitting up sentences into single words.
Definition
Tokenization is the process of segmenting the text into sequences of characters called tokens, which usually correspond to the words in the text (although sometimes we tokenize at the character level).
Tokenization requires language-specific resources (e.g., lexicons, morphological rules) and could be a challenging task for some languages. In order to create the tokens, it’s necessary to find a way to split the sentence into a sequence of words. The most common way to do this is to use space characters between words. For example, in English, at the beginning of each word, there is a space character. However, some languages, such as Chinese, don’t use spaces to separate words and it’s necessary to decide where the token boundaries should be.

Another big problem with tokenizing certain texts is that depending on the application, you may want to split hyphenated words. For example, “Italian-style furniture” should be split into “Italian”, “style”, “furniture”. Some languages are highly agglutinative and can build very long and specific content. For example, the word “hippopotomonstrosesquipedaliophobia” means “fear of monstrously long words” (literally: hippopotamus + monster + one-and-a-half + feet + fear). In German, “die Unabhängigkeitserklärung” means “the Declaration of Independence”, and in Italian, “incontrovertibilissimamente” means “in a way that is very difficult to falsify”. Sometimes the “unit of meaning” is spread over two non-hyphenated words. For example, “New York” should be split into “New_York”, a single token and not two separate words.
Sometimes, tokenization cannot blindly remove punctuation, for example in the case of “m.p.h.”, “Ph.D.”, “AT&T”, “cap’n”, prices ($45.55), dates (01/02/06), URLs (http://www.stanford.edu), hashtags (#nlproc), and email addresses…
Clitics, words that don’t stand on their own, should also be considered. For example, “are” in “we’re”, French “je” in “j’ai”, and “le” in “l’honneur”. Multiword expressions (MWE) should also be considered as single words. For example, “New York” and “rock ‘n’ roll”.
Examples of simple Tokenizers
The sci-kit learn library in Python contains one of the most commonly used tokenizers. The default tokenizer in sci-kit learn is a simple one that utilizes a regular expression to divide the text into individual words. The regular expression used is (?u)\b\w\w+\b, where \b matches word boundaries (start or end of a string), and \w matches any character considered a “word” character. This tokenizer is efficient and effective for basic word tokenization tasks in Python.
Another example of a tokenizer is the nltk.regexp_tokenize function. This function uses a more complex regular expression to split the text into words and catch various types of tokens.
pattern = r'''(?x) # set flag to allow verbose regexps
([A-Z]\.)+ # abbreviations, e.g. U.S.A.
|\w+(-\w+)* # words with optional internal hyphens
|\$?\d+(\.\d+)?%? # currency and percentages, e.g. $12.40, 82%
|\.\.\. # ellipsis
|[.,;"'?():-_`] # these are separate tokens; includes ], [Using this pattern, the text “That U.S.A. poster-print costs
In all the languages that do not use spaces to separate words, it is necessary to use a different approach to tokenize the text. Instead of white-space segmentation or single-character segmentation, it is possible to use sub word tokenization to tokenize the text. This method is useful for splitting up longer words and for allowing the machine learning model to learn explicitly the morphology of the language.
Example
For example, Chinese, contains 2.4 characters on average, so deciding what counts as a word can be difficult. Consider the sentence: “姚明进入总决赛” which means “Yao Ming reaches the finals”. This sentence can be tokenized at different levels:
- “姚明 进入 总决赛” (Yao Ming reaches finals),
- “姚 明 进入 总 决赛” (Yao Ming reaches overall finals),
- “姚 明 进 入 总 决 赛” (Yao Ming enter enter overall decision game).
In this case, it is common to just treat each character as a token. Other languages, like Thai and Japanese, require complex segmentation.
Sentence Segmentation
Certain tasks require sentences to be segmented. Punctuation marks like ”!” and ”?” often indicate the end of the statement/question, except for math expressions like "
The period ”.” is commonly used to end a sentence, but is very ambiguous since it also appears in abbreviations like Inc. or Dr. and numbers like
A common algorithm to segment sentences is to tokenize the text and then use rules (or machine learning) to classify a period as either part of the word or a sentence-boundary.
Word Frequencies
The problem of word frequencies is a fundamental one in NLP. The number of words in a sentence can be counted in many different ways. For example, the sentence “I mainly do uh, mainly business data processing” can be counted as
Definitions
A lemma is the same stem and part of speech, while a wordform is the full inflected surface form.
Usually, we distinguish between types and tokens. A type/term is an element of the vocabulary, while a token is an instance of that type in running text. For example, the sentence “She actively encouraged the discouraged child to act courageously and confront her fears” contains
In order to analyze the text, we can use statistical laws.
-
Heap’s law states that the vocabulary grows with approximately the square root of the document/collection length. The number of tokens is proportional to the square root of the number of types. The Heap’s law formula is
where . For example, the vocabulary of the Switchboard phone conversations contains million tokens and thousand types. 
-
Zipf’s law states that a token’s frequency is approximately proportional to the inverse of its rank. The Zipf’s law formula is
where . For example, the Google -grams collection contains 1 trillion tokens and 13+ million types. 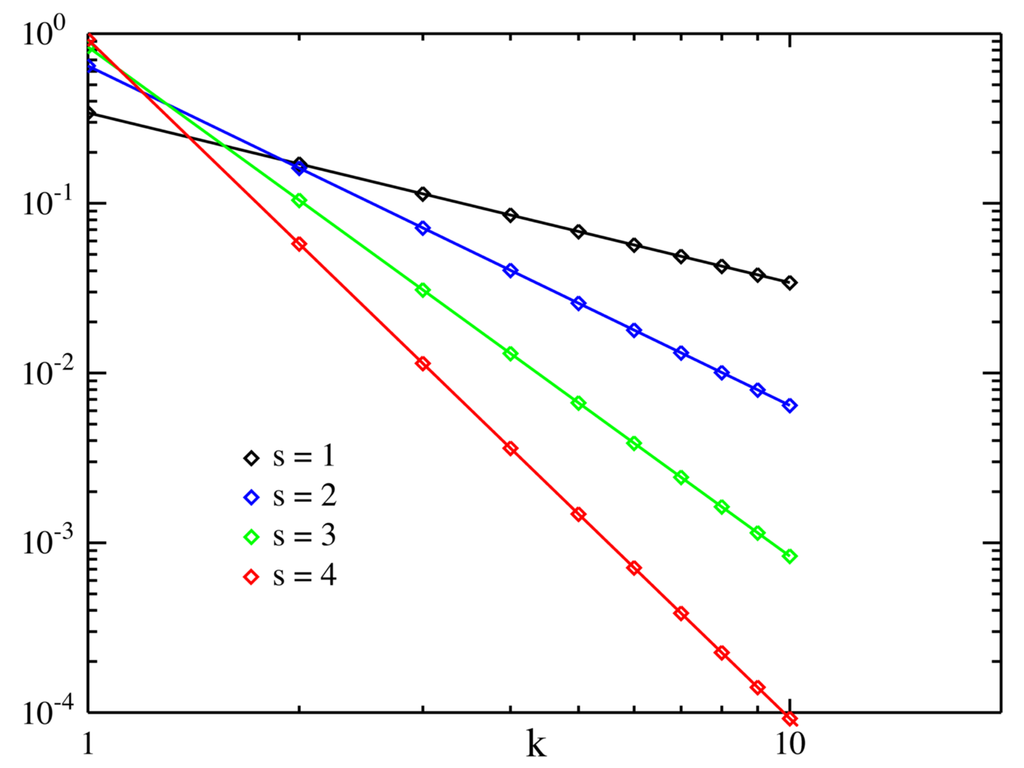
The table below shows examples of collections and their corresponding vocabularies.
| Collection | Tokens | Vocabulary |
|---|---|---|
| Switchboard phone conversations | 2.4 million | 20 thousand |
| Shakespeare | 884 thousand | 31 thousand |
| COCA | 440 million | 2 million |
| Google N-grams | 1 trillion | 13+ million |
The Heap’s law derives from Zipf’s law and can be explained by a random monkey typing. The monkey theorem states that a monkey hitting keys at random on a typewriter keyboard for an infinite amount of time will almost surely type any given text, such as the complete works of William Shakespeare. The probability of a monkey typing a given text is very low, but not zero (Infinite monkey theorem).
Normalizing Text
Application like web search often reduces all letters to lowercase. This drastically reduces the size of the vocabulary and increases the recall (the set of valid documents found). This is done also because users tend to use lowercase in search queries. For classification problems, removing case reduces the vocabulary and thus the number of parameters that must be learned, helping the classifier to generalize well from far fewer examples. However, sometimes we lose important information by removing case. For example, the word “who” might refer to the WHO (the World Health Organization), the Who (the rock band), or a person (who was being talked about). Thus, retaining case can be helpful for many applications like sentiment analysis, machine translation, and information extraction.
Definition
Word Normalization is the process of converting words/tokens into a standard format. This is a critical process for web search applications that could not present to you the correct documents if the query is in uppercase and the document is in lowercase.
Morphology
Definition
A morpheme is the smallest linguistic unit that has semantic meaning. For example, “unbelievably” is composed of the morphemes “un-”, “believe”, “-able-”, and “-ly”.
A morpheme can be divided in two parts: a root and affixes. The root is the base form, while the affixes are the prefix, infix, or suffix. Morphemes compose to make lexemes.
Definitions
- A lexeme is the unit of lexical meaning that exists regardless of the number of inflectional endings it may have or the number of words it may contain.
- A lemma is the canonical form of a lexeme.
- A lexicon is the set of lexemes.
- A word is, in general, an inflected form of a lexeme.
To compose morphemes, we need morphologic rules that restrict the ordering of morphemes, and orthographic rules that define how the morphemes are written. For example, the morphologic rule to create the plural noun is to add an “s” to the singular noun. Otherwise, the orthographic rule for create the plural of the word “fox” is to add an “es” to the word, and not just an “s”.
Lexicons are a very important component in NLP. They define the base forms, the affix morphemes, and address irregular forms.
Definitions
Lemmatization is the process of representing all words as their lemma, their shared root. For example, “am”, “are”, “is” and “be” are all lemmatized to “be”.
Stemming is a simple algorithm that reduces terms to stems, chopping off affixes crudely. It do not need to use lexicon and is often used in text retrieval to reduce computational requirements.
An important algorithm for stemming is the Porter Stemming Algorithm (1980). This algorithm uses a set of rewriting rules to reduce the terms to their stems. For example, the rule “+ATIONAL” is reduced to “+ATE” (e.g., “relational” is reduced to “relate”). However, this algorithm can have collisions, where different words have the same stem. For example, “correctional facilities” is reduced to “correct” and “facil”, while “facile corrections” is reduced to “facil” and “correct”.
In text retrieval, in order to prevent vocabulary mismatch between query and document, it is common to perform stemming (or lemmatization) before adding terms to the index. In this way, for example, all the versions of the word “car” (like “car”, “cars”, “car’s”, “cars’”) are reduced to the same lemma “car”.
The difference between stemming and lemmatization is that stemming is a simple algorithm that applies rules to extract word stems, while lemmatization is a more sophisticated NLP technique that uses vocabulary and morphological analysis to extract the lemma. Lemmatization can be important for morphologically rich languages (e.g., French).
Stopwords
TIP
Stopwords are just the most frequent terms in a language. They have extremely high document frequency scores (low discriminative power) and convey very little information about the topic of the text. For example, in English, common stopwords are “the”, “be”, “to”, “and”, “of”, “that”, “not”…
from nltk.corpus import stopwords
stop_words = sorted(list(set(stopwords.words('english'))))
print("\n".join(["\t".join(stop_words[i:i+6]) for i in range(0, len(stop_words), 6)]))Removing stopwords can sometimes boost the performance of retrieval/classification models, but more likely it will just reduce the computational/memory burden and speed up the index by removing massively long posting lists. Removing stopwords can sometimes be problematic, as they can be useful to understand the context of the text. For example, consider the rock band “the The” or the difference between “a white house” and “the white house”.
Spelling Correction
There can be many sources of errors in an extracted text file: most of the time they are introduced by Optical Character Recognition (OCR), especially for handwriting recognition. Another common cause of errors are the one made by humans, like spelling mistakes, typos, cognitive errors, and deliberate use by the author of non-existent words.
If the application requires it, it may be necessary to correct errors as part of the pre-processing pipeline. In case of a huge corpus of text, with every possible misspelled word, where authors had corrected every mis-spelling they’d ever written, it would be possible to estimate the probability of a correct word given an observed word.
Consider the sentence ”… stellar and versatile acress whose combination…” where the word “acress” is not a valid word in our vocabulary. What is the chance that writer intended to write “actress” instead (
In case of a really small corpus of text, we have to find other ways to estimate that probability. One way is to use the string edit distance, which counts the number of insertions, deletions, substitutions, or transpositions needed to get from one string to the other.
| Error | Correction | Correct letter | Error letter | Position (letter #) | Type |
|---|---|---|---|---|---|
| acress | actress | t | - | 2 | deletion |
| acress | cress | - | a | 0 | insertion |
| acress | caress | ca | ac | 0 | transposition |
| acress | access | c | r | 2 | substitution |
| acress | across | o | e | 3 | substitution |
| acress | acres | - | s | 5 | insertion |
| acress | acres | - | s | 5 | insertion |
then “acress”, “caress”, “cress”, “access”, “across”, “acres” would all be equally likely, but surely some of those words (like “actress”) are more likely than others (like “cress”)? We can use Bayes’ Rule to estimate the probability of a correct word given an observed word. We can write the condition the other way around:
where the dominator is the same for all the candidate correction, so we can ignore it and normalize the probability later:
where
For each possible correction, we need to estimate the likelihood (
- For the prior probability, we can see how popular that word is in a large corpus. For example, in a corpus of 44 million words, given
as the frequency of the word , we have: . 
- For the likelihood, we can estimate the probability of the observed word given the correct word (
) by counting in large corpus of errors how many times the observed word was typed instead of the correct word. Then, the confusion matrix can be used to estimate the probability of the observed word given the correct word, but we need an annotated corpus with the corrections. 
To make use of the context information, we can follow these steps:
- Look at the preceding words and see how much they agree with the candidate correction. For example, “versatile actress” sounds much more likely than “versatile acres”.
- Count the frequency of bigrams in a large corpus of documents. This helps us estimate the probability of the observed word given the correct word.
- Replace the unigram probability, such as
, with the bigram probability, such as . - By incorporating the observed context, the spelling correction can make better use of both the observed word and the surrounding words.
Naïve Bayes Classifier
By replacing the unigram probability
we have:
which is a form of Naïve Bayes model with two features: the observed word (incorrect) and the previous word (context).
