2.4 - Non Deterministic Models

---

In traditional deterministic algorithms, the sequence of operations is explicitly defined: given a particular input or configuration, the next step is always clearly determined. However, the concept of nondeterministic models of computation challenges this rigidity by introducing the idea that certain decision points within an algorithm could allow for multiple possible paths or choices. These choices are not predetermined, and the algorithm may follow any of them, offering potential advantages in terms of expressiveness, computational efficiency, or design flexibility.

Determinism vs. Nondeterminism

To illustrate the difference, consider the following deterministic code:

if x > y then 
  max := x 
else 
  max := y

In this example, the condition (x > y) fully determines which branch of the code will execute. The decision is entirely dependent on the specific values of x and y, leaving no ambiguity about the next step. This type of structure reflects the standard notion of an algorithm as a precise and predictable sequence of operations.

Now compare this with a nondeterministic version:

if  
  x >= y then 
	  max := x
  y >= x then 
	  max := y
fi

Here, the logic introduces a degree of flexibility. There is no strict “either-or” decision in the same way as the previous example, and both conditions are allowed to be true in parallel. Although this version may seem less elegant or intuitive, it opens the door to different execution pathways, particularly useful in certain computational contexts, such as parallelism.

One area where nondeterminism could enhance algorithm design is in control structures, like the case construct in Pascal and other programming languages. Traditionally, these constructs work deterministically, selecting one branch based on a specific condition. However, a nondeterministic case structure might look like this:

case
  x = y then S1
  z > y + 3 then S2
  ... then ...
endcase

In this version, multiple conditions could potentially be true at the same time, leading to different possible actions (e.g., S1, S2, etc.). The machine or algorithm could then choose one of the paths nondeterministically. This choice introduces flexibility, allowing for more dynamic or parallelizable algorithms.

Hidden Nondeterminism: The Example of Blind Search

A more subtle form of nondeterminism is often hidden in what are referred to as “blind search” algorithms, where the search process does not have complete information and must explore multiple paths.

Consider searching for an element in a binary tree.

• If the target element is at the root, the search completes immediately.
• If not, the algorithm can either search the left subtree or the right subtree. The choice of which subtree to explore first is arbitrary and can be made nondeterministically.

Here, traditional search algorithms can be thought of as simulations of nondeterministic algorithms. The search proceeds step by step, exploring one branch at a time, but the process of choosing which branch to explore is essentially arbitrary and could be paralleled. If two machines could explore both the left and right subtrees simultaneously, the search would complete faster. This suggests that nondeterminism can serve as a useful model for parallel computation.

Nondeterminism in computation is particularly valuable when considering parallelism and concurrent computing. Many modern programming languages that support concurrency, such as Ada, exploit nondeterminism to model parallel processes. In such languages, tasks can be assigned to different processors or threads, executing simultaneously without a predefined sequence. For example, consider a scenario in which multiple tasks or computational paths are equally likely to yield a solution. In a nondeterministic model:

• You could assign different tasks to different processors.
• Each processor could work on its task without waiting for the others, with the system nondeterministically selecting the first solution to complete.

This is essentially what happens in systems that support concurrent execution. The ability to run tasks in parallel without dictating a strict order of operations allows for greater flexibility and can significantly improve performance in multi-core or distributed systems.

Although purely nondeterministic machines do not exist in real-world computing (because physical machines must always follow a deterministic sequence of instructions), nondeterminism remains a powerful theoretical tool. It is used extensively in computational theory, particularly in the study of nondeterministic finite automata (NFA) and nondeterministic Turing Machines (NTM), which help us understand concepts such as:

• vs. : The class of problems solvable in polynomial time by a deterministic machine () versus those solvable in polynomial time by a nondeterministic machine ().
• Parallelism and concurrency: The study of how tasks can be executed in parallel to improve efficiency, which is often modeled using nondeterministic algorithms.

Nondeterminism provides an abstract framework that allows us to think about computation differently, challenging the conventional deterministic model and opening new possibilities for more flexible, efficient, and scalable designs.

Nondeterministic Automaton (NDA)

In a nondeterministic automaton (NDA), the transition function, denoted as , describes the sequence of moves the automaton can take when processing an input string. The notation refers to the set of all possible states that the NDFA can reach after starting in state and processing the input string .

In the transition diagram provided:

graph LR
 A((q1)) -- a --> B((q2)) -- b --> C((q4))
 B -- b --> D((q5))
 A -- a --> E((q3)) -- b --> D
 E -- b --> F((q6))

We can observe that state branches into two states, and , upon reading the same input symbol . This illustrates the fundamental characteristic of nondeterminism: for a given state and input, there can be multiple possible next states.

Formula

The formal description of these transitions can be written as:

This means that after reading the symbol in state , the automaton could transition either to state or state .

Following these transitions:

Thus, when reading the next symbol :

• If the automaton is in state , it may move to either or .
• If the automaton is in state , it may move to either or .

We can now define the transition for the string “ab”:

This means that after reading the string “ab” starting from state , the automaton could be in any of the states , , or .

Definition

The recursive definition of , which describes how an NDA processes a string (where is a substring and is a single input symbol), is:

This states that if the automaton reads the empty string , it remains in its current state .

For a non-empty string, , we have:

This means that the automaton first processes the substring and reaches a set of possible states. For each state in that set, it applies the transition function for the symbol , and the result is the union of all possible resulting states.

An NDA accepts an input string if, after processing the entire string, there is at least one computation path that leads the automaton to an accepting state.

Definition

Formally, this is expressed as:

where:

• represents the set of states that the automaton can reach after starting in the initial state and processing the string .
• is the set of accepting states.

The string is accepted if the set of reachable states contains at least one state from the accepting set .

In the traditional interpretation of nondeterminism, referred to as existential nondeterminism, the automaton accepts an input string if at least one of the possible runs succeeds in reaching an accepting state.

Alternatively, in universal nondeterminism, the automaton accepts the input string only if all possible runs (i.e., all computation paths) lead to accepting states. In this case, the acceptance condition would be:

This means that every possible state reached by the automaton after processing the string must be an accepting state.

Universal nondeterminism is much stricter than existential nondeterminism and is often associated with models of computation that guarantee the correctness of all parallel execution paths.

Nondeterministic Finite-State Automata (NFA)

NFAs (Nondeterministic Finite-State Automata) are finite-state machines where for a given state and input symbol, the automaton can transition to multiple possible states.

Example of an NFA

Consider the following NFA with multiple transitions:

graph LR
 subgraph 1[ ]
  q1((q1))
 end
 subgraph 2[ ]
  q2((q2))
  q3((q3))
 end
 subgraph 3[ ]
  q4((q4))
  q5((q5))
  q6((q6))
 end

 q1 -- a --> q2 -- b --> q4
 q2-- b --> q5
 q1 -- a --> q3-- b --> q5
 q3 -- b --> q6

Starting in state , upon reading the input , the automaton can transition to any of the states in the set , depending on the path taken. This nondeterminism means that multiple valid paths exist, and the automaton accepts if any path leads to an accepting state.

Definition

An NFA is a 5-tuple

where:

• is a finite set of states.
• is the input alphabet.
• is the transition function, mapping , where is the power set of (i.e., the set of all possible subsets of ).
• is the start state.
• is the set of accepting states.

The extended transition function describes how the NFA processes a string . For any state , the function returns the set of possible states after reading the string:

If at least one of the states after processing the input string is an accepting state, the automaton accepts the input.

An NFA accepts an input string if:

This means that if any of the possible states after processing belong to the set of accepting states , the NFA accepts the input.

Another, alternative interpretation of nondeterminism: universal nondeterminism (the previous one is existential) all runs of the automaton accept

Determinization: NFA to DFA

Though NFAs are nondeterministic, it is always possible to convert any NFA into an equivalent deterministic finite automaton (DFA). The key difference between the two is that the DFA must explicitly track all possible states that the NFA could be in at any point.

Algorithm

Given an NFA , we can build an equivalent DFA by following these steps:

1. States of the DFA: The DFA’s states are the power set of the NFA’s states, i.e., .

2. Transition function: For each state and input symbol , the transition function is defined as:

   This means that for each subset of the NFA’s states, the DFA transitions to the union of the possible next states of each individual NFA state in .

3. Start state: The start state of the DFA is the set containing the start state of the NFA: .

4. Accepting states: The DFA’s accepting states are those that include at least one of the NFA’s accepting states:

Thus, any NFA can be converted into a DFA that accepts the same language, though the DFA may have up to states, which can lead to an exponential blow-up in the number of states.

Even though NFAs and DFAs are equivalent in terms of the languages they accept (i.e., both accept regular languages), NFAs are often preferred in certain scenarios for practical reasons:

1. Ease of Design: NFAs are often easier to design and conceptualize. For example, when constructing an automaton for a specific pattern-matching problem, it is often easier to describe the behavior using nondeterminism and then convert it to a DFA later if needed.
2. Efficient Computation: Despite the potential exponential increase in the number of states, there are efficient algorithms (like subset construction) to convert an NFA into a DFA when necessary. In some cases, the overhead of working directly with an NFA is justified, particularly if the NFA has fewer states than the equivalent DFA.
3. Applications in Regular Expressions: NFAs play a crucial role in the implementation of regular expressions, where nondeterminism helps efficiently match patterns against text. Regular expressions, which are equivalent to finite automata, are often converted to NFAs before being processed or compiled into deterministic forms.

Example

Consider two example languages:

• : Strings over the alphabet where the symbol before the last one is .
• : Strings where the fourth symbol before the last one is .

In these cases, it is often easier to describe and design an NFA to accept these languages, and then determinize it if necessary.

Nondeterministic Pushdown Automaton (NPDA)

Pushdown automata (PDA) are naturally nondeterministic by design, allowing multiple possible transitions for a given input, state, and stack symbol. This ability makes them more expressive than deterministic PDA (DPDA), particularly for certain language classes.

Example of Nondeterminism in PDA

In the transition diagram below:

graph LR
 A((q1)) -- i,A/α --> B((q2))
 A -- ɛ,A/β --> C((q3))

the PDA has two possible transitions from state , depending on whether it reads an input symbol or the empty symbol , and on the stack’s current symbol . The key feature of an NPDA is that multiple transitions can occur from the same state and input configuration:

graph LR
 A((q1)) -- i,A/α --> B((q2))
 A -- i,A/β --> C((q3))

This nondeterministic behavior allows the automaton to explore multiple computation paths simultaneously.

Transition Function for NPDA

Definition

The formal transition function for NPDA is given by:

where:

• is the set of states.
• is the input alphabet.
• is the stack alphabet.
• denotes the set of finite subsets (we restrict the automaton to finite sequences of moves to avoid infinite branching).

The transition function returns a set of possible states and stack configurations based on the current state, input symbol, and top stack symbol.

An NPDA accepts a string if there exists a sequence of configurations:

This means that starting from an initial configuration , there exists a finite sequence of transitions (denoted ) leading to an accepting configuration, where:

• is an accepting state.
• The input string has been entirely consumed (denoted by ).
• The stack is in some configuration .

Example: NPDA Accepting

Consider the NPDA that accepts the language . The nondeterministic nature of the automaton allows it to guess whether it should proceed to accept or , leading to two distinct computational paths.

In this NPDA:

• One path accepts strings of the form by matching each with a corresponding .
• Another path accepts strings of the form by pushing two ‘s for each .

Consequences of Nondeterminism in NPDA

1. More Powerful Than DPDA: Nondeterministic PDA can accept certain languages that deterministic PDA cannot. For example, the language , which cannot be accepted by any PDA (deterministic or nondeterministic), illustrates the limitations of PDA even with nondeterminism, but other complex languages are NPDA-acceptable.

2. Closure Properties:

   • NPDA are closed under union, meaning that given two NPDAs and , we can construct a new NPDA that accepts . This is not the case for DPDA, which are not closed under union.
   • NPDA are not closed under intersection or complement. For instance, the language , which can be written as the intersection of two context-free languages, cannot be accepted by an NPDA.

3. Complementation: Nondeterminism complicates complementation. In deterministic models, complementation can often be achieved by swapping accepting and non-accepting states, but for NPDA, this strategy does not work. For example, there may be two computation paths: In this case, the string is accepted even if one path leads to rejection. Complementation does not simply involve flipping accept and reject states because both paths must be considered.

Nondeterminism and Power of Automata

Nondeterminism generally increases the power of an automaton. For example:

• NFA vs DFA: Nondeterministic finite automata and deterministic finite automata are equivalent in terms of the languages they can accept (regular languages). However, NFA can be more concise than DFA.
• NPDA vs DPDA: Nondeterministic pushdown automata can accept a larger class of languages than DPDA (context-free languages vs deterministic context-free languages).

The key question remains: for other kinds of automata (like Turing machine), does nondeterminism increase the computational power? In the case of Turing machines, nondeterminism does not increase the class of problems they can solve (since both deterministic and nondeterministic Turing machines recognize the same class of languages—recursively enumerable), but it can impact complexity, particularly in the time it takes to solve problems.

Nondeterministic Turing Machines (NTM)

A Nondeterministic Turing Machine (NTM) is an extension of the classical Turing machine that allows for multiple possible transitions from a given state, input symbol, and tape configuration. NTMs are conceptual tools that help us understand the limits of computation and how nondeterminism affects computational models.

Definition

An NTM can be defined as a 7-tuple:

where:

• is a finite set of states.
• is the input alphabet.
• is the tape alphabet, with .
• is the transition function: . Here, represents the number of tapes (usually in standard models).
• is the initial state.
• is the set of accepting states.
• is the reject state, which is implicitly included.

The machine has several tapes, each of which can read/write symbols and move left (), right (), or stay in place (). Nondeterminism is introduced by allowing the transition function to map to a set of possible states, tape configurations, and movements. This means that from a given state and tape symbol, the NTM can make multiple different transitions, branching out into different computation paths.

Computation Tree

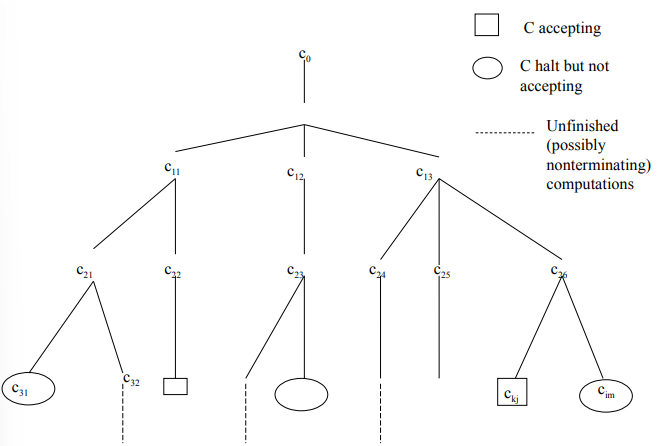
When an NTM is given an input string, its computation can be represented as a computation tree, where each node represents a configuration of the machine, and each branch represents a possible transition. The machine accepts an input if there exists at least one path in the computation tree that leads to an accepting state. In other words, if any of the branches of the computation tree leads to an accepting state, the NTM accepts the input. This existential form of nondeterminism (where one successful computation suffices for acceptance) is key to the power of NTMs.

Example

Consider an NTM that accepts the language . The NTM can branch nondeterministically after reading a string of ‘s to guess when to switch to reading the ‘s. It can then nondeterministically match the ‘s with the previously read ‘s, accepting the string if the counts match.

The critical question is whether NTMs can solve more problems than deterministic Turing machines (DTMs). The answer is no in terms of computational power—NTMs are no more powerful than DTMs. Every NTM can be simulated by a DTM, which means that any problem solvable by an NTM can also be solved by a DTM.

However, the difference lies in efficiency:

• Nondeterministic TMs can guess the correct path of computation and solve problems in fewer steps, essentially exploring multiple computation paths in parallel.
• Deterministic TMs, on the other hand, need to simulate all possible paths sequentially, which may result in an exponential increase in time complexity.

A deterministic Turing machine can simulate an NTM by exploring all the branches of the NTM’s computation tree. There are two main strategies for exploring the tree:

1. Depth-First Search (DFS): The machine explores one branch of the tree as deeply as possible before backtracking and trying another branch. However, if the tree has infinite branches, DFS can get stuck in an infinite loop without ever finding a successful accepting path.
2. Breadth-First Search (BFS): The machine explores the tree level by level, ensuring that every possible branch is considered equally. BFS avoids getting stuck in infinite paths and ensures that the machine eventually finds an accepting path if one exists.