Polimi CS - Notes

2.2 - Pushdown Automata

11 min read

  • pushdown automata
  • PDA
  • pushdown automaton

Pushdown Automata (PDA) extend the capabilities of finite state automata by incorporating a memory structure known as a stack. This stack allows the automaton to handle a broader range of computational problems, particularly those involving context-free languages, such as balancing parentheses or matching patterns with nested structures.

A pushdown automaton (PDA) is a computational model that can be thought of as a finite state machine with an additional stack memory. This stack enables the automaton to store and retrieve information in a last-in, first-out (LIFO) manner through push (inserting an item) and pop (removing an item) operations. Unlike finite state machines (FSM), which have limited memory, PDAs can recognize patterns and structures that require tracking an arbitrary number of elements.

A pushdown automaton operates based on:

  • Input symbols: The symbols being read from the input tape.
  • Stack symbols: The symbol currently on top of the stack.
  • Current state: The active state of the control unit.

The pushdown automaton changes its state, moves ahead the scanning head (or it does not if the input was ignored), changes the symbol read on top of the stack with a string of symbols ( may be empty: this amounts to a pop operation of ). If the pushdown automaton is used as a translator, it writes a string (possibly empty) on the output tape (advancing the writing head consequently).

The input string is recognized (accepted) if the automaton scans it completely (the scanning head reaches the end of ), and upon reaching the end of it’s in a acceptance state (just like for the FA). If the automaton is also a translator, the is the string on the output tape after has been accepted (if is accepted, otherwise is undefined: ).

is the "undefined" symbol, but not in any alphabet: is just a shorthand for .

Accepting

Consider the language , which consists of strings where the number of ‘a’s is equal to the number of ‘b’s. A PDA can be designed to accept this language by pushing symbols onto the stack when encountering ‘a’s and popping them off when encountering ‘b’s. The process ensures that the number of ‘a’s matches the number of ‘b’s.

The move do not read anything but simply perform a pop of and a push of . This move is called -move (or spontaneous move). The symbol is overloaded: used as an additional input symbol but it’s not a symbol: .

Definition

A pushdown automaton is defined as:

where:

  • is the finite set of states
  • is the finite set of input symbols
  • is the finite set of stack symbols
  • is the initial state

The function , defined as

is a partial function (just like for the FA).

graph LR
    q((q)) -- a,A / α,w --> p((p))

where , with , , and .

Pushdown Automaton as Traslator

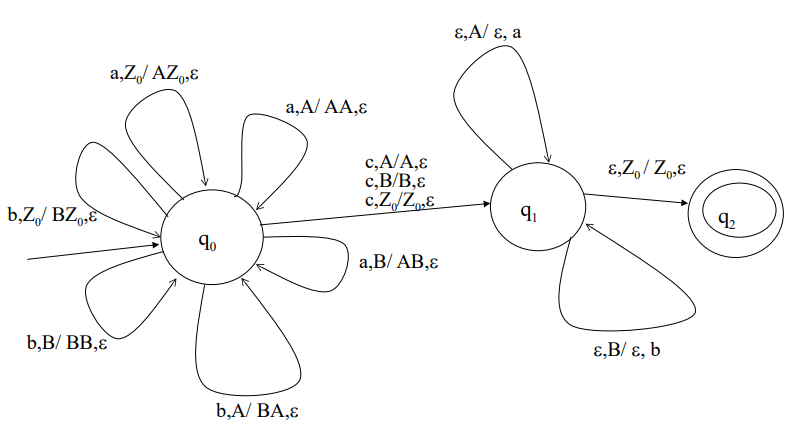
This automaton, given the input alphabet, when receive a word like it translates it into (the reverse of ). For example, a word like "" will be translated into "", ignoring any character.

Definition

A pushdown automaton as a translator is defined as:

where is the output alphabet and is the output function. The function , defined as

This function is a partial function (just like ) that associates to each transition a string of output symbols.

A configuration is a generalization of the notion of state, and it’s defined as where:

  • is the state of the control device
  • is the unread portion of the input string (the head is positioned on the first symbol of )
  • is the string of symbols in the stack (by convention )
  • is the string written (up to now) on the output tape

Transition Relation

The transition relation is a formal way to describe how the pushdown automaton moves from one configuration to another.

Definition

A configuration captures the current state of the PDA, the unread portion of the input, the current stack content, and any output generated so far.

Here, the configuration consists of:

  • : The current state of the control unit.
  • : The current input symbol being read.
  • : The unread portion of the input string (i.e., the input tape head is positioned on , and the rest is unread).
  • : The stack content, with as the top symbol and as the rest of the stack.
  • : The string that has been written on the output tape up to now.

The configuration represents the new state after applying a transition:

  • : The new state.
  • : The updated unread portion of the input string.
  • : The updated stack, where replaces .
  • : The updated output string, where is written to the output.

We can have two possible scenarios

  1. Input-Consuming Transition If (where ), the PDA consumes the input symbol and moves forward with the rest of the unread string , so . In this case, the PDA reads the input, processes the top of the stack, changes its state, updates the stack, and possibly writes to the output tape.

  2. -Move (Spontaneous Transition) If (where ), the PDA performs an -move, meaning it transitions without consuming any input. In this case, the unread portion remains . An -move allows the PDA to change states, update the stack, and possibly generate output without reading any input symbol.

The condition ensures that the transition function is always defined for any combination of states and symbols.

This implies that -moves are alternative to transitions that consume input, ensuring non-determinism does not arise when both -moves and input-consuming transitions are possible at the same time.

The relation denotes the reflexive and transitive closure of , meaning that it represents zero or more steps of the transition relation:

  • Reflexive: The PDA can remain in the same configuration without performing any transitions.
  • Transitive: The PDA can move from one configuration to another through a sequence of transitions.

A string is accepted by the PDA if there exists a sequence of transitions from the initial configuration to a final configuration:

This means:

  • is accepted if, starting from the initial state , reading the entire input , and starting with an empty stack , the PDA can reach an accepting state after consuming the input.
  • At the same time, , meaning the output string is the translation of the input , and it is written on the output tape.

In the final configuration, denotes that the input string has been fully consumed, and (the stack content) is immaterial, as it doesn’t affect the acceptance of the string.

When processing the input string, especially at the end, it is crucial to account for any possible final -moves. These moves allow the PDA to manipulate the stack or change states without consuming input, potentially leading to an accepting state.

Properties of Pushdown Automata

  1. Acceptance of Language Pushdown automata are capable of accepting context-free languages that require a form of balancing or counting, such as the language . This language represents a sequence of ’s followed by ’s, where the number of ’s must match the number of ’s exactly. The PDA achieves this by:
    • Pushing an onto the stack for every encountered.
    • Popping an from the stack for every encountered.
    By the time all ’s are processed, the stack is empty, and the input string is accepted if the automaton is in an accepting state.

Limitations of PDA: Language ⁿⁿⁿ

Pushdown automata are not capable of accepting languages like , where there are three distinct symbols and the counts of each symbol must match. The limitation arises because a PDA has only one stack, which cannot be used to count three different quantities simultaneously. Specifically:

  • After counting ’s and ’s, the stack becomes empty, and there is no memory left to count ’s.
  • This limitation can be formally proven through the pumping lemma for context-free languages.
  1. Acceptance of Language The language can be accepted by a pushdown automaton. In this case, the PDA pushes ’s onto the stack and pops the stack for the first ’s. The automaton then accepts after encountering an additional ’s. This shows that PDAs can handle languages where certain segments of the input are counted multiple times or where specific patterns are required.

Limitations: Language

The language cannot be accepted by a pushdown automaton. This is because:

  • If the PDA empties its stack after processing ’s, it cannot count the remaining ’s from the second part of the language .
  • Similarly, if the PDA only partially empties the stack and encounters fewer ’s than expected, it cannot determine whether it is halfway through the stack.
  • This limitation also follows from the pumping lemma for context-free languages.

The class of languages accepted by PDAs, denoted as , exhibits certain closure properties:

  • Not closed under union: For example, is not context-free.
  • Not closed under intersection: PDAs cannot recognize languages that require simultaneous checking of two properties.
  • Not closed under complement: To take the complement of a context-free language, we must change accepting states into non-accepting states, but this does not always yield a valid PDA for the complement language.

Handling ε-Moves and Nondeterminism

PDAs often utilize -moves (spontaneous transitions that do not consume input symbols). However, these moves can lead to nondeterminism, where the automaton can enter infinite loops of -transitions, never reaching the end of the input string. To avoid this, the PDA must be carefully designed to prevent infinite cycles, especially when using -moves at the end of the input.

For instance, after a sequence of transitions like:

the PDA must “force” acceptance only after a finite sequence of -moves, ensuring that the automaton halts properly.

PDAs as Acceptors and Translators

PDAs can be viewed either as acceptors (recognizing languages) or translators (converting input strings into output strings). While PDAs are more powerful than finite automata due to their ability to use a stack, they still have limitations compared to more powerful machines like Turing machines:

  • Unlimited counting ability: PDAs can count but not indefinitely. For example, they can process nested structures but only to a finite depth.
  • Limited memory: Unlike Turing machines, which have infinite memory, PDAs can only access the top of the stack, and each time they read from the stack, they destroy its content.

Pumping Lemma for Context-Free Languages

The pumping lemma is a key tool for proving that certain languages are not context-free (and thus not recognizable by PDAs). It shows that:

  • Context-free languages can be “pumped” or decomposed into substrings in such a way that repeating certain parts of the string still results in a valid string within the language.
  • If a language fails the pumping lemma for context-free languages, it cannot be recognized by a PDA.

Backlinks

Graph View